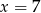Środek 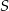 okręgu o równaniu
okręgu o równaniu 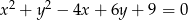 ma współrzędne
ma współrzędne
A) 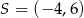 B)
B) 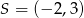 C)
C) 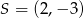 D)
D) 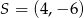
/Szkoła średnia/Zadania testowe
Środkiem okręgu o równaniu 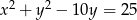 jest punkt
jest punkt
A) 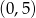 B)
B) 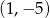 C)
C) 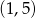 D)
D) 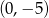
Środek okręgu o równaniu 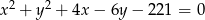 ma współrzędne
ma współrzędne
A) 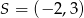 B)
B) 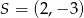 C)
C) 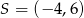 D)
D) 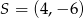
Środek 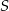 okręgu o równaniu
okręgu o równaniu 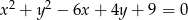 ma współrzędne
ma współrzędne
A) 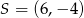 B)
B) 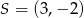 C)
C) 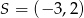 D)
D) 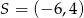
Środek 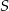 okręgu o równaniu
okręgu o równaniu 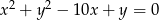 ma współrzędne
ma współrzędne
A) 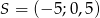 B)
B) 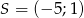 C)
C) 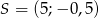 D)
D) 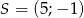
Środek 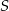 okręgu o równaniu
okręgu o równaniu 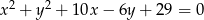 ma współrzędne
ma współrzędne
A) 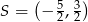 B)
B) 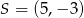 C)
C) 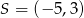 D)
D) 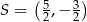
Środek 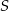 okręgu o równaniu
okręgu o równaniu 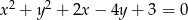 ma współrzędne
ma współrzędne
A) 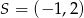 B)
B) 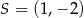 C)
C) 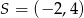 D)
D) 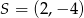
Kąt  jest ostry i
jest ostry i 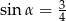 . Wówczas
. Wówczas
A) 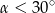 B)
B) 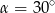 C)
C) 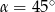 D)
D) 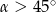
Kąt  jest ostry i
jest ostry i 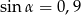 . Wówczas
. Wówczas
A) 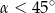 B)
B) 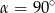 C)
C) 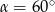 D)
D) 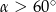
Kąt  jest ostry oraz
jest ostry oraz 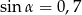 . Zatem
. Zatem
A) 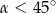 B)
B) 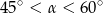 C)
C) 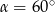 D)
D) 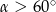
Jeśli  jest kątem ostrym i
jest kątem ostrym i 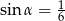 , to
, to
A) 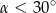 B)
B) 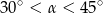 C)
C) 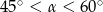 D)
D) 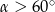
Zbiór 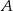 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 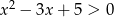 . Zatem
. Zatem
A) 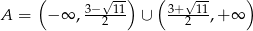 B)
B) 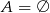 C)
C) 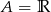 D)
D) 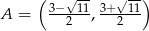
Zbiór 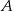 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 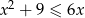 . Zatem
. Zatem
A) 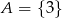 B)
B) 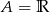 C)
C) 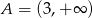 D)
D) 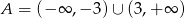
Zbiór 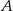 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 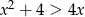 . Zatem
. Zatem
A) 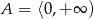 B)
B) 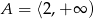 C)
C) 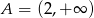 D)
D) 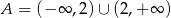
Zbiór 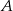 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 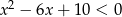 . Zatem
. Zatem
A) 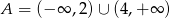 B)
B) 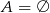 C)
C) 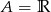 D)
D) 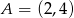
Zbiór 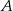 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 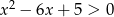 . Zatem
. Zatem
A) 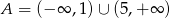 B)
B) 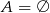 C)
C) 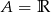 D)
D) 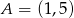
Zbiór 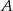 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 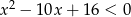 . Zatem
. Zatem
A) 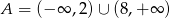 B)
B) 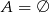 C)
C) 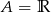 D)
D) 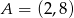
Dana jest funkcja kwadratowa 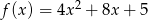 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 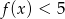 jest
jest
A) 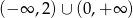 B)
B) 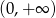 C)
C) 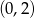 D)
D) 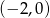
Zbiorem rozwiązań nierówności 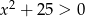 jest
jest
A) 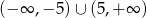 B)
B) 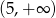 C)
C) 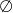 D)
D) 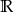
Do zbioru rozwiązań nierówności 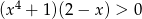 nie należy liczba
nie należy liczba
A) 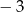 B)
B) 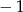 C) 1 D) 3
C) 1 D) 3
Do zbioru rozwiązań nierówności 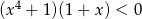 nie należy liczba
nie należy liczba
A) 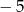 B)
B) 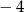 C)
C) 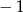 D)
D) 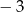
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe 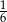 , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 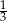 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 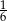 B)
B) 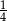 C)
C) 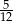 D)
D) 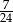
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 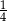 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 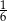 B)
B) 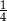 C)
C) 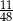 D)
D) 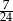
Punkt 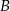 jest symetryczny do punktu
jest symetryczny do punktu 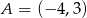 względem osi
względem osi 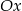 układu współrzędnych, a punkt
układu współrzędnych, a punkt 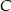 jest symetryczny do punktu
jest symetryczny do punktu 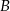 względem osi
względem osi 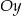 . Zatem trójkąt
. Zatem trójkąt 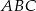 jest
jest
A) równoboczny
B) prostokątny i równoramienny
C) prostokątny i żaden z jego kątów nie jest równy 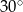
D) prostokątny z kątem ostrym równym 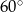
W kwadracie 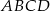 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 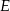 i
i 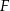 na bokach
na bokach 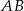 i
i 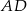 w ten sposób, że odcinek
w ten sposób, że odcinek 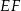 jest równoległy do przekątnej
jest równoległy do przekątnej 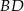 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
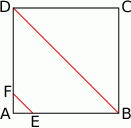
Długość odcinka 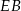 jest równa
jest równa
A) 12 B) 15 C) 14 D) 16
Dany jest czterowyrazowy ciąg arytmetyczny 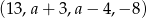 . Wynika stąd, że
. Wynika stąd, że
A) 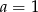 B)
B) 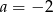 C)
C) 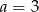 D)
D) 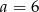
Funkcja 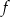 określona jest wzorem
określona jest wzorem 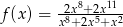 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 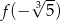 jest równa
jest równa
A) 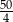 B)
B) 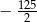 C)
C) 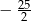 D)
D) 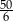
W trójkącie prostokątnym przeciwprostokątna ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 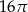 B)
B) 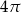 C)
C) 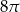 D)
D) 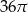
Pole koła opisanego na trójkącie prostokątnym o bokach długości 10, 24, 26 jest równe
A) 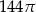 B)
B) 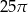 C)
C) 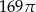 D)
D) 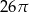
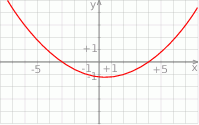
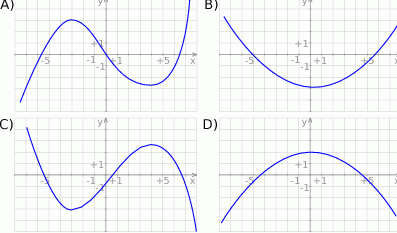
Rysunek przedstawia wykres funkcji 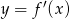 .
.
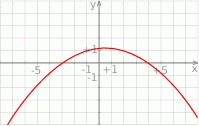
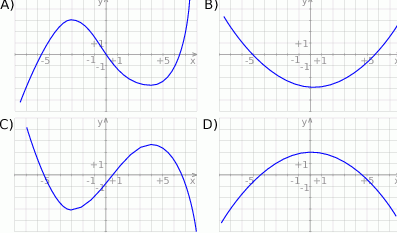
Wskaż wykres funkcji 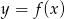 .
.
Rysunek przedstawia wykres funkcji 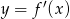 .
.
Wskaż wykres funkcji 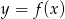 .
.
Wszystkich liczb całkowitych dodatnich spełniających nierówność 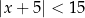 jest
jest
A) 9 B) 10 C) 20 D) 21
Wszystkich liczb całkowitych ujemnych spełniających nierówność 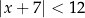 jest
jest
A) 19 B) 23 C) 18 D) 24
Liczba wszystkich dodatnich liczb pięciocyfrowych, które są podzielne przez 3, i których cyfry należą do zbioru 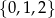 , jest równa
, jest równa
A) 81 B) 54 C) 162 D) 243
Wzór funkcji liniowej, której wykresem jest prosta nachylona do osi 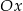 pod kątem o mierze
pod kątem o mierze 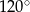 i przechodzi przez punkt
i przechodzi przez punkt 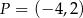 jest postaci
jest postaci
A) 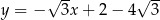 B)
B) 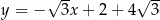
C) 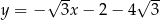 D)
D) 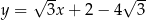
Wykres funkcji liniowej 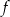 jest nachylony do osi
jest nachylony do osi 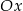 pod kątem
pod kątem 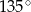 . Wiadomo, że
. Wiadomo, że 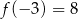 . Funkcja liniowa
. Funkcja liniowa 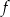 jest określona wzorem
jest określona wzorem
A) 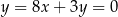 B)
B) 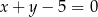
C) 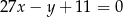 D)
D) 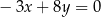
Objętość sześcianu jest równa 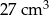 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 18 cm B) 36 cm C) 24 cm D) 12 cm
Objętość sześcianu jest równa 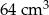 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 48 cm B) 36 cm C) 24 cm D) 64 cm
Dane są dwie funkcje liniowe określone wzorami 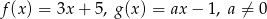 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 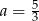 B)
B) 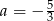 C)
C) 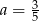 D)
D) 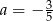
Dane są dwie funkcje liniowe określone wzorami 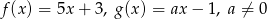 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 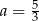 B)
B) 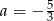 C)
C) 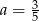 D)
D) 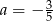
Funkcja liniowa 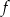 określona wzorem
określona wzorem 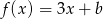 ma takie samo miejsce zerowe, jakie ma funkcja liniowa
ma takie samo miejsce zerowe, jakie ma funkcja liniowa 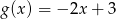 . Stąd wynika, że
. Stąd wynika, że
A) 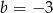 B)
B) 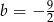 C)
C) 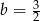 D)
D) 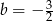
Dane są dwie funkcje liniowe określone wzorami 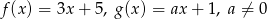 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 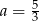 B)
B) 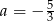 C)
C) 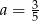 D)
D) 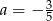
Funkcja liniowa 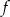 określona wzorem
określona wzorem 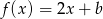 ma takie samo miejsce zerowe, jakie ma funkcja liniowa
ma takie samo miejsce zerowe, jakie ma funkcja liniowa 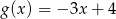 . Stąd wynika, że
. Stąd wynika, że
A) 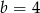 B)
B) 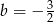 C)
C) 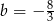 D)
D) 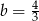
Funkcje liniowe 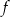 i
i 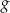 określone wzorami
określone wzorami 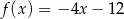 i
i 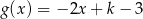 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 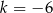 B)
B) 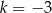 C)
C) 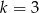 D)
D) 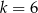
Funkcje liniowe 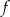 i
i 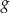 określone wzorami
określone wzorami 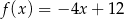 i
i 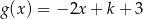 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 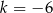 B)
B) 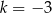 C)
C) 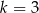 D)
D) 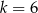
Liczba  jest odwrotnością liczby
jest odwrotnością liczby 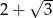 , zaś
, zaś 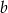 jest liczbą przeciwną do liczby
jest liczbą przeciwną do liczby 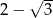 . Różnica
. Różnica 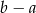 jest wówczas równa:
jest wówczas równa:
A) 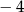 B)
B) 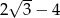 C)
C) 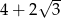 D) 0
D) 0
Liczba punktów wspólnych wykresu funkcji wymiernej 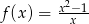 z osią
z osią 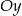 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych wykresu funkcji wymiernej 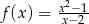 z osią
z osią 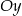 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
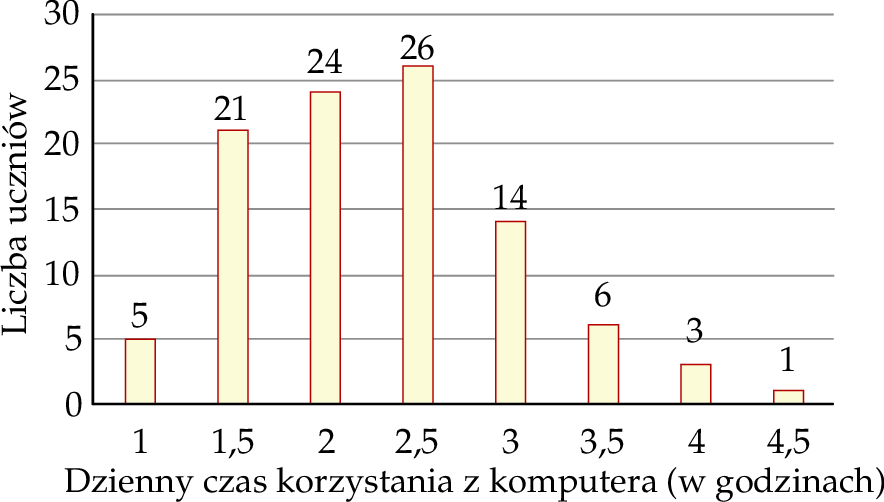
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 2,75 godziny D) 1,50 godziny
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
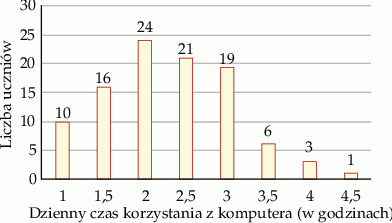
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 1,5 godziny D) 2 godziny
Jeżeli 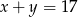 i
i 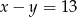 to
to
A) 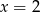 B)
B) 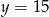 C)
C) 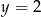 D)
D) 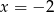
Jeżeli 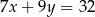 i
i 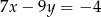 to
to
A) 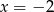 B)
B) 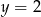 C)
C) 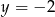 D)
D)