Zadanie nr 5717183
Funkcja 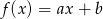 dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
A) 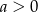 B)
B) 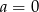 C)
C) 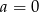 i
i 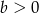 D)
D) 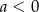
Rozwiązanie
Sposób I
Prosta będącą wykresem opisanej funkcji musi być powyżej osi dla 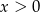 i poniżej osi dla
i poniżej osi dla 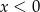 . Wynika stąd, że prosta ta musi przechodzić przez punkt
. Wynika stąd, że prosta ta musi przechodzić przez punkt 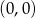 i mieć dodatni współczynnik kierunkowy (musi być rosnąca).
i mieć dodatni współczynnik kierunkowy (musi być rosnąca).
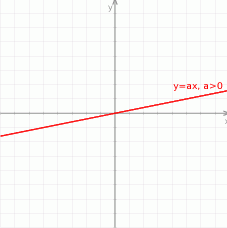
Sposób II
Od razu odpadają odpowiedzi B i C, bo wtedy funkcja jest stała, więc nie może jednocześnie przyjmować wartości dodatnich i ujemnych. Jeżeli 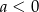 to dla dużych wartości
to dla dużych wartości  wyrażenie
wyrażenie 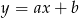 jest ujemne, co jest sprzeczne z założeniem, że funkcja ma mieć dodatnie wartości dla liczb dodatnich. Pozostaje zatem odpowiedź A.
jest ujemne, co jest sprzeczne z założeniem, że funkcja ma mieć dodatnie wartości dla liczb dodatnich. Pozostaje zatem odpowiedź A.
Odpowiedź: A

