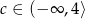Układ równań 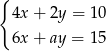 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 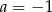 B)
B) 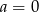 C)
C) 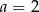 D)
D) 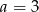
/Szkoła średnia/Zadania testowe/Równania
Układ równań 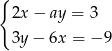 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 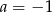 B)
B) 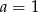 C)
C) 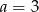 D)
D) 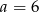
Układ równań 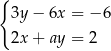 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 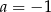 B)
B) 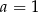 C)
C) 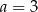 D)
D) 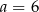
Układ równań 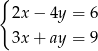 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 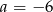 B)
B) 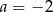 C)
C) 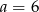 D)
D) 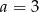
Układ równań 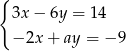 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 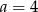 B)
B) 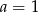 C)
C) 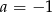 D)
D) 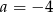
Rozwiązaniem równania 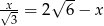 jest liczba
jest liczba
A) 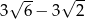 B)
B) 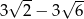 C)
C) 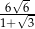 D)
D) 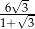
Funkcja liniowa określona jest wzorem 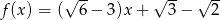 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 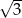 B)
B) 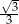 C)
C) 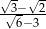 D)
D) 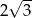
Rozwiązaniem równania 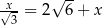 jest liczba
jest liczba
A) 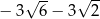 B)
B) 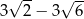 C)
C) 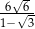 D)
D) 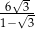
Liczba rozwiązań równania 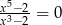 jest równa
jest równa
A) 0 B) 1 C) 2 D) 5
Liczba rozwiązań równania 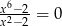 jest równa
jest równa
A) 6 B) 3 C) 2 D) 1
Iloczyn liczb spełniających równanie 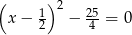 jest równy
jest równy
A) 6 B) 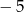 C) 5 D)
C) 5 D) 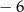
Funkcja kwadratowa określona jest wzorem 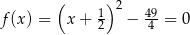 . Liczby
. Liczby 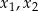 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 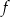 . Zatem
. Zatem
A) 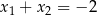 B)
B) 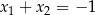 C)
C) 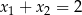 D)
D) 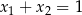
Para liczb 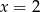 i
i 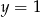 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 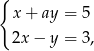 gdy
gdy
A) 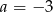 B)
B) 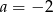 C)
C) 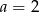 D)
D) 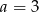
Para liczb 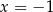 i
i 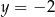 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 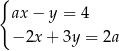 dla
dla
A) 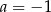 B)
B) 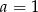 C)
C) 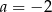 D)
D) 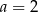
Para liczb 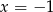 i
i 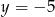 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 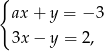 gdy
gdy
A) 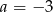 B)
B) 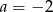 C)
C) 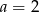 D)
D) 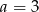
Para liczb 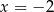 i
i 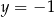 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 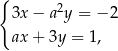 dla
dla
A) 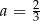 B)
B) 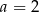 C)
C) 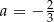 D)
D) 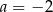
Para liczb 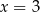 ,
, 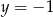 spełnia układ równań
spełnia układ równań
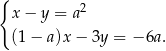
Wtedy  jest równe
jest równe
A) 2 B) 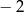 C)
C) 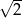 D)
D) 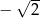
Para liczb 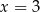 i
i 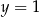 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 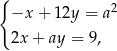 dla
dla
A) 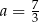 B)
B) 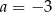 C)
C) 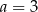 D)
D) 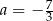
Para liczb 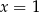 ,
, 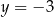 spełnia układ równań
spełnia układ równań
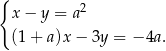
Wtedy  jest równe
jest równe
A) 2 B) 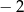 C)
C) 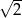 D)
D) 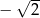
Para liczb 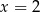 i
i 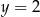 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 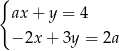 dla
dla
A) 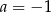 B)
B) 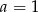 C)
C) 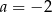 D)
D) 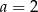
Interpretacją geometryczną układu równań 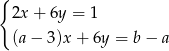 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 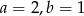 B)
B) 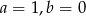 C)
C) 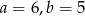 D)
D) 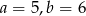
Interpretacją geometryczną układu równań 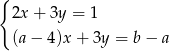 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 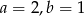 B)
B) 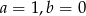 C)
C) 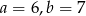 D)
D) 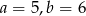
Interpretacją geometryczną układu równań 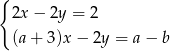 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 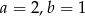 B)
B) 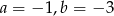 C)
C) 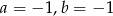 D)
D) 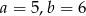
Jeżeli 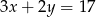 i
i 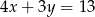 to
to
A) 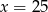 B)
B) 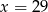 C)
C) 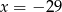 D)
D) 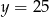
Jeżeli 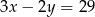 i
i 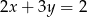 to
to
A) 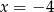 B)
B) 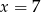 C)
C) 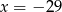 D)
D) 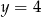
Ile pierwiastków ma wielomian 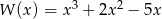 ?
?
A) 0 B) 1 C) 2 D) 3
Ile różnych pierwiastków ma wielomian 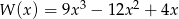 ?
?
A) 0 B) 1 C) 2 D) 3
Równanie 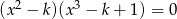 nie ma rozwiązań niewymiernych. Liczba
nie ma rozwiązań niewymiernych. Liczba 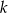 może być równa
może być równa
A) 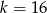 B)
B) 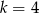 C)
C) 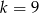 D)
D) 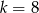
Jeżeli 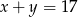 i
i 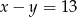 to
to
A) 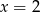 B)
B) 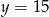 C)
C) 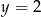 D)
D) 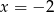
Jeżeli 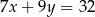 i
i 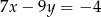 to
to
A) 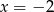 B)
B) 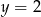 C)
C) 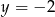 D)
D) 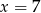
Trójka liczb 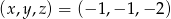 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 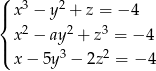 gdy
gdy
A) 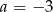 B)
B) 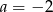 C)
C) 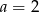 D)
D) 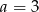
Trójka liczb 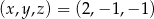 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 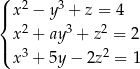 gdy
gdy
A) 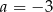 B)
B) 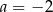 C)
C) 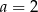 D)
D) 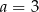
Równanie 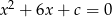 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 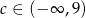 B)
B) 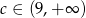 C)
C) 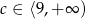 D)
D) 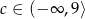
Równanie 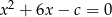 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 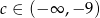 B)
B) 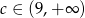 C)
C) 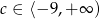 D)
D) 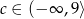
Równanie 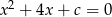 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 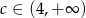 B)
B) 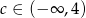 C)
C) 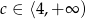 D)
D)