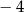Najmniejszym rozwiązaniem równania 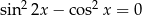 w przedziale
w przedziale 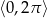 jest liczba
jest liczba
A) 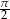 B)
B) 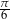 C)
C) 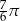 D)
D) 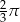
/Szkoła średnia/Zadania testowe/Równania
Rozwiązaniem układu równań 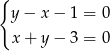 jest para
jest para
A) 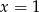 i
i 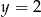 B)
B) 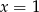 i
i 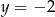 C)
C) 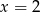 i
i 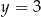 D)
D) 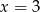 i
i 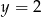
Rozwiązaniem układu równań 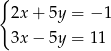 jest
jest
A) 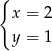 B)
B) 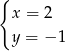 C)
C) 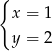 D)
D) 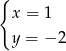
Rozwiązaniem układu równań 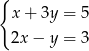 jest
jest
A) 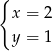 B)
B) 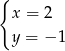 C)
C) 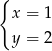 D)
D) 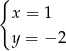
Rozwiązaniem układu równań 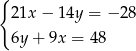 jest para liczb
jest para liczb
A) 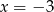 i
i 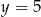 B)
B) 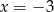 i
i 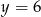 C)
C) 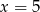 i
i 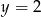 D)
D) 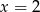 i
i 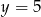
Dany jest układ równań
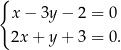
Rozwiązaniem tego układu równań jest para liczb
A) 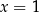 i
i 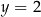 B)
B) 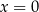 i
i 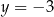 C)
C) 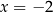 i
i 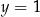 D)
D) 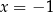 i
i 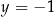
Dany jest układ równań
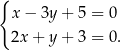
Rozwiązaniem tego układu równań jest para liczb
A) 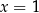 i
i 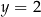 B)
B) 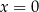 i
i 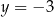 C)
C) 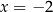 i
i 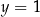 D)
D) 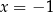 i
i 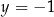
Układ równań 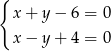 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt
A) 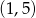 B)
B) 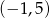 C)
C) 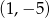 D)
D) 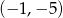
Rozwiązaniem układu równań 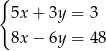 jest para liczb
jest para liczb
A) 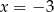 i
i 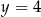 B)
B) 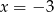 i
i 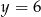 C)
C) 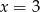 i
i 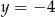 D)
D) 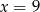 i
i 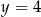
Rozwiązaniem układu równań 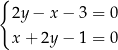 jest para
jest para
A) 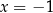 i
i 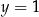 B)
B) 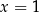 i
i 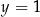 C)
C) 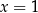 i
i 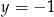 D)
D) 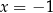 i
i 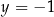
Jednym z pierwiastków równania 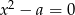 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 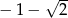 . Zatem liczba
. Zatem liczba  jest równa:
jest równa:
A) 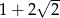 B)
B) 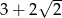 C)
C) 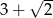 D) 0
D) 0
Układ równań 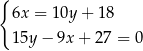
A) ma dokładnie jedno rozwiązanie. B) ma dwa rozwiązania.
C) ma nieskończenie wiele rozwiązań. D) nie ma rozwiązań.
Układ równań 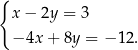
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 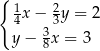
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 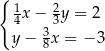
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 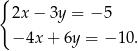
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 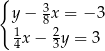
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 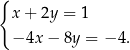
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 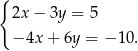
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Równanie 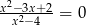 ma:
ma:
A) 2 pierwiastki B) 3 pierwiastki C) 1 pierwiastek D) 4 pierwiastki
Wszystkimi rozwiązaniami równania wymiernego 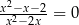 są
są
A) 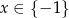 B)
B) 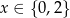 C)
C) 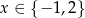 D)
D) 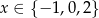
Rozwiązaniami równania 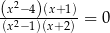 są liczby
są liczby
A) 2 B) 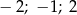 C)
C) 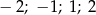 D)
D) 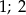
Równanie
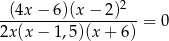
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 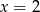 .
.
B) dokładnie dwa rozwiązania: 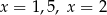 .
.
C) dokładnie trzy rozwiązania: 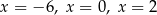 .
.
D) dokładnie cztery rozwiązania: 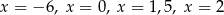 .
.
Równanie
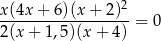
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 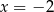 .
.
B) dokładnie dwa rozwiązania: 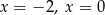 .
.
C) dokładnie trzy rozwiązania: 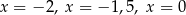 .
.
D) dokładnie cztery rozwiązania: 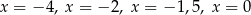 .
.
Liczba 3 jest rozwiązaniem równania
A) 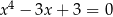 B)
B) 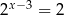 C)
C) 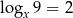 D)
D) 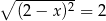
Miejscem zerowym funkcji liniowej 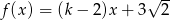 jest liczba
jest liczba 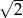 jeśli
jeśli
A) 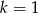 B)
B) 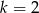 C)
C) 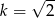 D)
D) 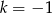
Liczba rozwiązań równania 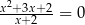 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Rozwiązaniem równania 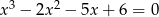 nie jest liczba
nie jest liczba
A) 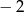 B) 1 C) 4 D) 3
B) 1 C) 4 D) 3
Miejscem zerowym funkcji 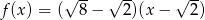 jest
jest
A) 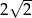 B)
B) 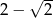 C)
C) 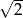 D)
D) 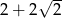
Miejscem zerowym funkcji 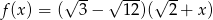 jest
jest
A) 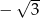 B)
B) 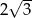 C)
C) 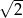 D)
D) 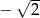
Miejscami zerowymi funkcji kwadratowej 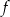 określonej wzorem
określonej wzorem 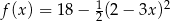 są liczby
są liczby
A) 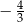 oraz
oraz 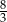 B)
B) 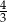 oraz
oraz 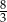 C)
C) 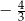 oraz
oraz 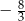 D)
D) 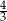 oraz
oraz 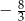
Równanie 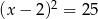 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Równanie 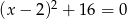 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Suma wszystkich pierwiastków równania 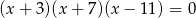 jest równa
jest równa
A) 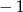 B) 21 C) 1 D)
B) 21 C) 1 D) 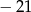
Suma wszystkich rozwiązań równania 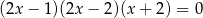 jest równa
jest równa
A) 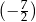 B)
B) 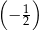 C)
C) 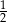 D) 1
D) 1
Suma wszystkich rozwiązań równania 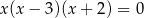 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Iloczyn wszystkich pierwiastków równania 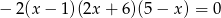 jest równy
jest równy
A) 15 B) 30 C) 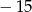 D)
D) 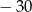
Suma wszystkich pierwiastków równania 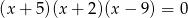 jest równa
jest równa
A) 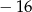 B) 2 C) 16 D)
B) 2 C) 16 D) 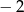
Suma wszystkich rozwiązań równania 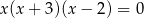 jest równa
jest równa
A) 0 B) 1 C) 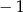 D) 6
D) 6
Rozwiązaniem równania 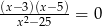 jest liczba:
jest liczba:
A) 3 B) -5 C) 5 D) 0
Rozwiązaniem równania 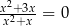 jest liczba
jest liczba
A) 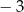 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Rozwiązaniem równania 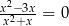 jest liczba
jest liczba
A) 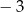 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Pary liczb 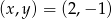 i
i 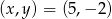 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 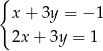 B)
B) 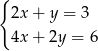 C)
C) 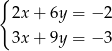 D)
D) 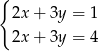
Pary liczb 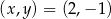 i
i 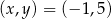 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 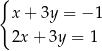 B)
B) 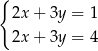 C)
C) 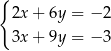 D)
D) 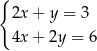
Układ liczb 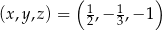 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
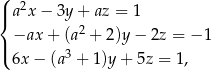
dla
A) 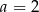 B)
B) 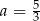 C)
C) 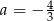 D)
D) 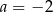
Równanie 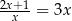
A) ma dwa rozwiązania: 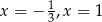 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 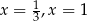
C) nie ma żadnego rozwiązania D) ma tylko jedno rozwiązanie 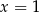
Równanie 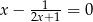
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Równanie 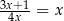
A) ma dwa rozwiązania: 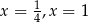 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 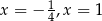
C) ma dwa rozwiązania: 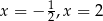 D) ma tylko jedno rozwiązanie
D) ma tylko jedno rozwiązanie 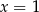
Równanie 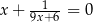
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Rozwiązaniem równania 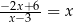 jest
jest
A) 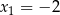 B)
B) 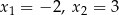 C)
C) 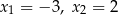 D)
D) 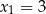
Liczba 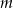 , dla której rozwiązaniem równania
, dla której rozwiązaniem równania 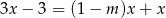 jest
jest 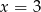 wynosi
wynosi
A) 3 B) 2 C) 1 D) 0
Rozwiązaniem równania 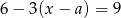 z niewiadomą
z niewiadomą  jest liczba 2. Zatem
jest liczba 2. Zatem
A) 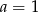 B)
B) 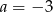 C)
C) 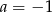 D)
D) 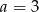
Liczba 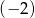 jest pierwiastkiem równania
jest pierwiastkiem równania 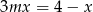 . Wtedy
. Wtedy
A) 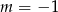 B)
B) 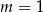 C)
C) 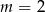 D)
D) 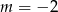
Suma rozwiązań równania 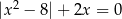 jest równa
jest równa
A) 0 B) 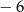 C) 2 D)
C) 2 D)