Równanie 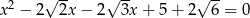
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
/Szkoła średnia/Zadania testowe/Równania
Iloczyn wszystkich rozwiązań równania 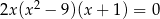 jest równy
jest równy
A) 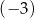 B) 3 C) 0 D) 9
B) 3 C) 0 D) 9
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
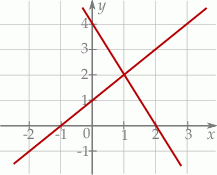
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 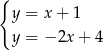 B)
B) 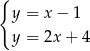 C)
C) 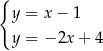 D)
D) 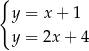
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
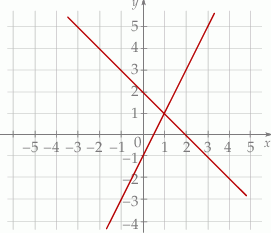
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 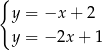 B)
B) 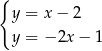 C)
C) 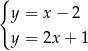 D)
D) 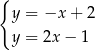
Na rysunku, w kartezjańskim układzie współrzędnych 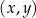 , przedstawiono interpretację geometryczną jednego z poniższych układów równań
, przedstawiono interpretację geometryczną jednego z poniższych układów równań
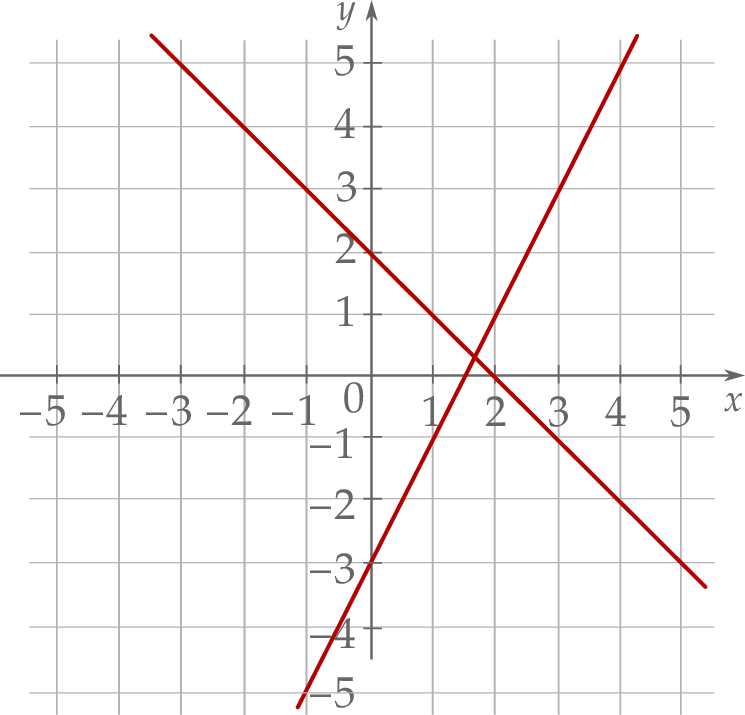
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 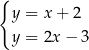 B)
B) 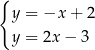 C)
C) 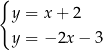 D)
D) 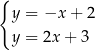
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 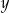 .
.
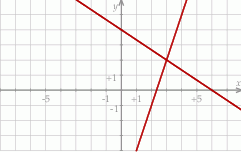
Wskaż ten układ
A) 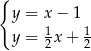 B)
B) 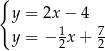 C)
C) 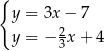 D)
D) 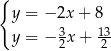
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
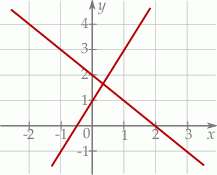
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 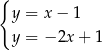 B)
B) 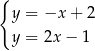 C)
C) 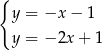 D)
D) 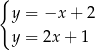
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
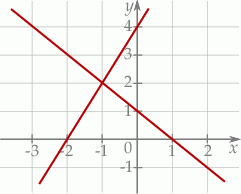
Wskaż ten układ
A) 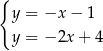 B)
B) 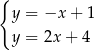 C)
C) 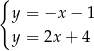 D)
D) 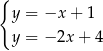
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
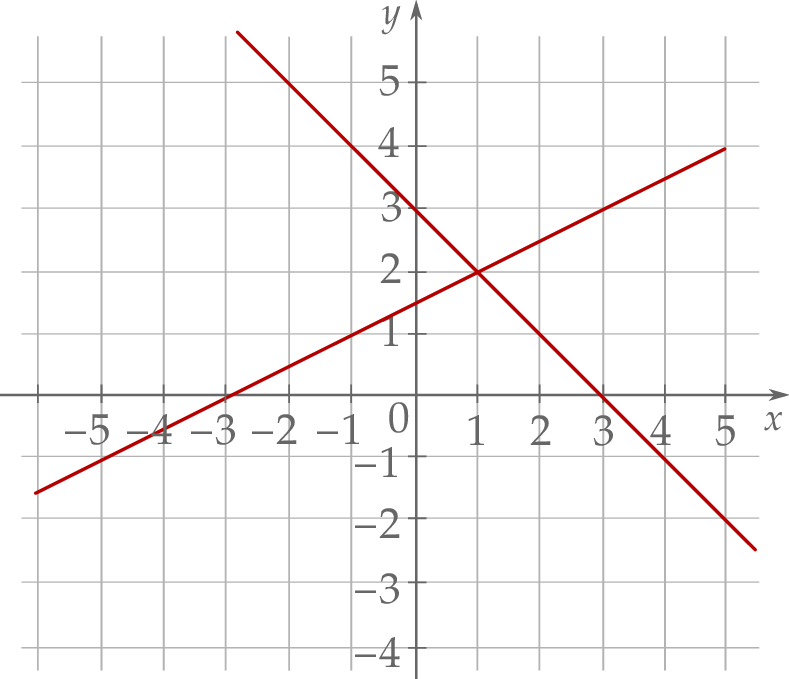
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 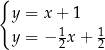 B)
B) 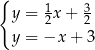 C)
C) 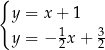 D)
D) 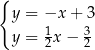
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 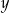 .
.
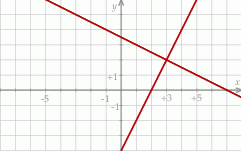
Wskaż ten układ
A) 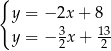 B)
B) 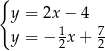 C)
C) 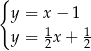 D)
D) 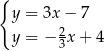
Na rysunku, w kartezjańskim układzie współrzędnych 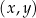 , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
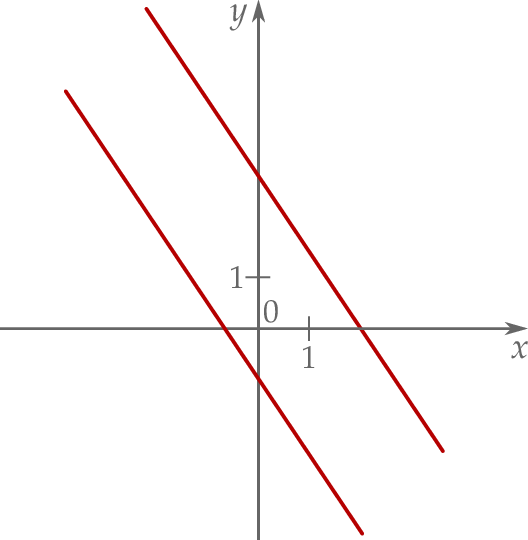
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 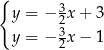 B)
B) 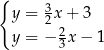
C) 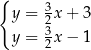 D)
D) 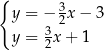
Liczba rozwiązań równania 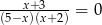 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba rozwiązań równania 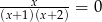 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 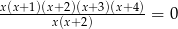 jest równa
jest równa
A) 6 B) 5 C) 4 D) 3
Liczba miejsc zerowych funkcji 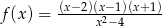 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 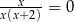 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Wskaż liczbę rozwiązań równania 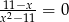 .
.
A) 0 B) 1 C) 2 D) 3
Równanie 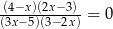 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Równanie 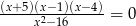
A) nie ma pierwiastków
B) ma jeden pierwiastek
C) ma dwa pierwiastki
D) ma trzy pierwiastki
Równanie 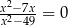 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 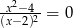
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Równanie 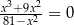 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 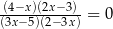 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Równanie 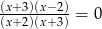 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 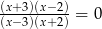 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 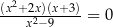 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) cztery rozwiązania. B) trzy rozwiązania.
C) dwa rozwiązania. D) jedno rozwiązanie.
Równanie 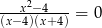
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 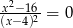
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 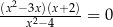 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 4 i 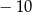 , można opisać za pomocą równania
, można opisać za pomocą równania
A) 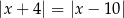 B)
B) 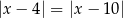
C) 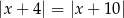 D)
D) 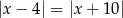
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 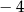 i 10, można opisać za pomocą równania
i 10, można opisać za pomocą równania
A) 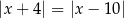 B)
B) 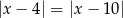
C) 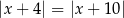 D)
D) 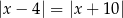
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 5 i 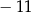 , można opisać za pomocą równania
, można opisać za pomocą równania
A) 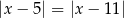 B)
B) 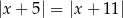
C) 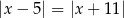 D)
D) 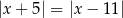
Liczba 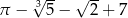 jest rozwiązaniem równania
jest rozwiązaniem równania 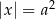 z niewiadomą
z niewiadomą  . Która z podanych liczb jest również rozwiązaniem tego równania?
. Która z podanych liczb jest również rozwiązaniem tego równania?
A) 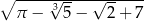 B)
B) 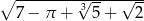
C) 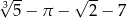 D)
D) 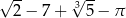
Funkcje liniowe 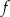 oraz
oraz 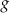 , określone wzorami
, określone wzorami 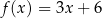 oraz
oraz 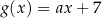 , mają to samo miejsce zerowe. Współczynnik
, mają to samo miejsce zerowe. Współczynnik  we wzorze funkcji
we wzorze funkcji 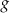 jest równy
jest równy
A) 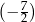 B)
B) 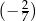 C)
C)  D)
D) 
Rozwiązaniem równania 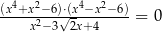 nie jest liczba
nie jest liczba
A) 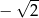 B)
B) 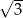 C)
C) 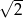 D)
D) 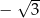
Rozwiązanie równania 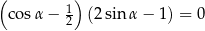 w przedziale
w przedziale 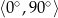 , to
, to
A) 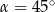 lub
lub 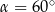 B)
B) 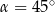 lub
lub 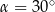
C) 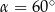 lub
lub 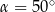 D)
D) 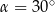 lub
lub 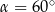
Liczba 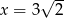 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 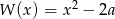 , gdy
, gdy  jest równe
jest równe
A) 18 B) 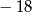 C) 9 D)
C) 9 D) 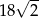
Układ równań 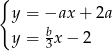 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 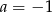 i
i 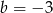 B)
B) 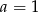 i
i 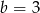 C)
C) 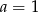 i
i 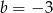 D)
D) 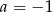 i
i 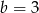
Układ równań 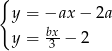 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 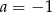 i
i 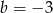 B)
B) 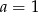 i
i 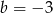 C)
C) 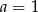 i
i 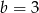 D)
D) 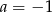 i
i 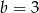
Jednym z rozwiązań równania 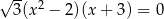 jest liczba
jest liczba
A) 3 B) 2 C) 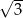 D)
D) 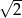
Jednym z rozwiązań równania 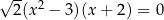 jest liczba
jest liczba
A) 3 B) 2 C) 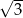 D)
D) 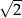
Rozwiązaniem równania 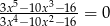 jest liczba
jest liczba
A) 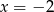 B)
B) 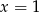 C)
C) 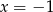 D)
D) 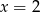
Jednym z pierwiastków równania 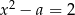 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 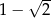 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 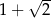 B)
B) 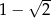 C)
C) 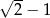 D) 0
D) 0
Zbiorem wszystkich rozwiązań równania 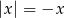 jest
jest
A) 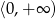 B)
B) 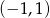 C)
C) 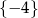 D)
D) 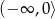
Zbiorem wszystkich rozwiązań równania 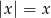 jest
jest
A) 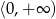 B)
B) 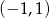 C)
C) 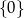 D)
D) 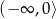
Układ równań 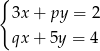 z niewiadomymi
z niewiadomymi  i
i 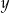 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 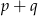 jest równa
jest równa
A) 6 B) 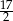 C)
C) 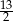 D) 15
D) 15
Układ równań 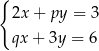 z niewiadomymi
z niewiadomymi  i
i 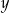 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 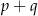 jest równa
jest równa
A) 6 B) 1 C) 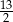 D)
D) 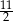
Równanie 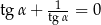 , gdzie
, gdzie  jest kątem ostrym
jest kątem ostrym
A) ma dokładnie jedno rozwiązanie B) ma dokładnie dwa rozwiązania
C) ma nieskończenie wiele rozwiązań D) nie ma rozwiązań
Suma pierwiastków wielomianu 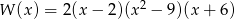 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Suma pierwiastków wielomianu 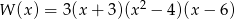 jest równa
jest równa
A) 3 B) 7 C) -7 D) -3
Suma wszystkich pierwiastków równania: 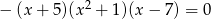 jest równa
jest równa
A) 0 B) 2 C) 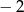 D) 1
D) 1
Suma pierwiastków wielomianu 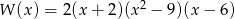 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Wskaż równanie, dla którego suma wszystkich rozwiązań jest równa 0.
A) 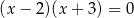 B)
B) 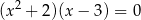
C) 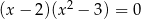 D)
D) 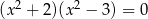
Równanie 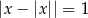 ? ma
? ma
A) nieskończenie wiele rozwiązań. B) jedno rozwiązanie.
C) dwa rozwiązania. D) zero rozwiązań.

