Równanie
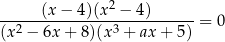
z niewiadomą  nie ma rozwiązań rzeczywistych. Liczba
nie ma rozwiązań rzeczywistych. Liczba  jest więc równa
jest więc równa
A) 6,5 B) 4 C) 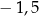 D)
D) 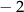
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Równanie
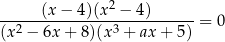
z niewiadomą  nie ma rozwiązań rzeczywistych. Liczba
nie ma rozwiązań rzeczywistych. Liczba  jest więc równa
jest więc równa
A) 6,5 B) 4 C) 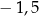 D)
D) 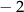
Liczby rzeczywiste 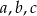 spełniają warunki:
spełniają warunki: 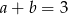 ,
, 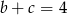 i
i 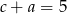 . Wtedy suma
. Wtedy suma 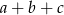 jest równa
jest równa
A) 20 B) 6 C) 4 D) 1
Liczby rzeczywiste 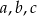 spełniają warunki:
spełniają warunki: 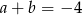 ,
, 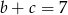 i
i 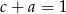 . Wtedy suma
. Wtedy suma 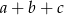 jest równa
jest równa
A) 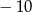 B) 8 C) 4 D) 2
B) 8 C) 4 D) 2
Jednym z rozwiązań równania 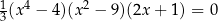 jest liczba
jest liczba
A) 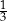 B)
B) 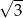 C)
C) 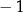 D)
D) 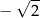
Liczba 1 jest miejscem zerowym funkcji liniowej 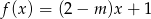 . Wynika stąd, że
. Wynika stąd, że
A) 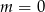 B)
B) 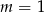 C)
C) 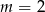 D)
D) 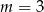
Liczba 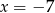 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 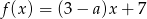 dla
dla
A) 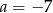 B)
B) 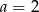 C)
C) 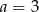 D)
D) 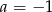
Liczba 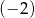 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 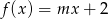 . Wtedy
. Wtedy
A) 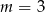 B)
B) 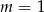 C)
C) 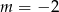 D)
D) 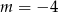
Miejscem zerowym funkcji liniowej 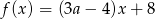 jest liczba 2. Liczba
jest liczba 2. Liczba  jest równa
jest równa
A) 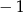 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Dla jakiej wartości parametru  , miejscem zerowym funkcji
, miejscem zerowym funkcji 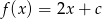 jest liczba
jest liczba 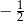 ?
?
A) 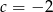 B)
B) 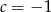 C)
C) 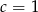 D)
D) 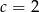
Liczba 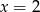 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 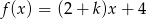 dla
dla
A) 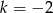 B)
B) 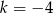 C)
C) 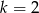 D)
D) 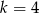
Liczba -1 jest miejscem zerowym funkcji liniowej 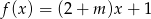 . Wynika stąd, że
. Wynika stąd, że
A) 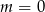 B)
B) 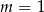 C)
C) 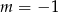 D)
D) 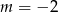
Miejscem zerowym funkcji liniowej 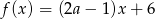 jest liczba 2. Liczba
jest liczba 2. Liczba  jest równa
jest równa
A) 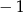 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Liczba 4 jest miejscem zerowym funkcji liniowej 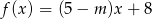 . Wynika stąd, że
. Wynika stąd, że
A) 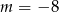 B)
B) 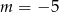 C)
C) 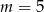 D)
D) 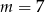
Jeśli miejscem zerowym funkcji 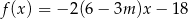 jest liczba 3, to wynika stąd, że
jest liczba 3, to wynika stąd, że
A) 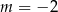 B)
B) 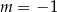 C)
C) 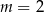 D)
D) 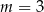
Miejscem zerowym funkcji 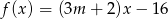 jest liczba
jest liczba 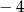 . Wynika stąd, że
. Wynika stąd, że
A) 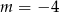 B)
B) 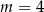 C)
C) 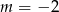 D)
D) 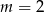
Miejscem zerowym funkcji liniowej 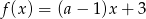 jest liczba
jest liczba 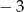 . Liczba
. Liczba  jest równa
jest równa
A) 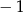 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Miejscem zerowym funkcji liniowej 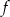 określonej wzorem
określonej wzorem 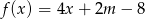 jest liczba -2. Zatem
jest liczba -2. Zatem 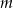 równa się
równa się
A) -6 B) 4 C) -2 D) 8
Liczba 2 jest miejscem zerowym funkcji liniowej 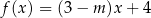 . Liczba
. Liczba 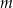 jest równa
jest równa
A) 0 B) 3 C) 4 D) 5
Miejsce zerowe funkcji liniowej 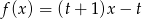 jest równe 2. Wynika stąd, że
jest równe 2. Wynika stąd, że
A) 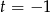 B)
B) 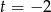 C)
C) 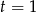 D)
D) 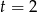
Funkcja 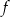 jest określona wzorem
jest określona wzorem 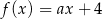 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba 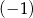 . Wtedy
. Wtedy
A) 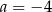 B)
B) 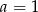 C)
C) 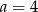 D)
D) 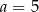
Funkcja 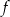 jest określona wzorem
jest określona wzorem 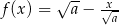 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba 8. Wtedy
. Miejscem zerowym tej funkcji jest liczba 8. Wtedy
A) 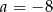 B)
B) 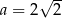 C)
C) 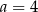 D)
D) 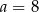
Liczba 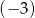 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 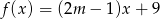 . Wtedy
. Wtedy
A) 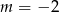 B)
B) 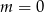 C)
C) 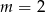 D)
D) 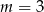
Liczba 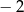 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 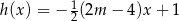 . Wynika stąd, że
. Wynika stąd, że
A) 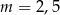 B)
B) 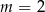 C)
C) 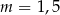 D)
D) 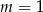
Funkcja liniowa 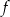 jest określona wzorem
jest określona wzorem 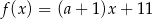 , gdzie
, gdzie  to pewna liczba rzeczywista, ma miejsce zerowe równe
to pewna liczba rzeczywista, ma miejsce zerowe równe 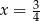 . Stąd wynika, że
. Stąd wynika, że
A) 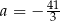 B)
B) 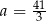 C)
C) 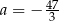 D)
D) 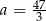
Miejscem zerowym funkcji liniowej 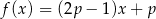 jest liczba
jest liczba 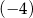 . Wtedy
. Wtedy
A) 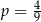 B)
B) 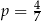 C)
C) 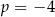 D)
D) 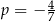
Liczba 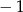 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 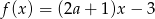 . Wynika stąd, że
. Wynika stąd, że
A) 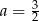 B)
B) 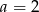 C)
C) 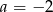 D)
D) 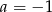
Funkcja 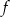 określona jest wzorem
określona jest wzorem 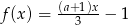 . Liczba
. Liczba 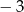 jest miejscem zerowym tej funkcji dla
jest miejscem zerowym tej funkcji dla  równego:
równego:
A) 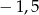 B)
B) 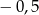 C)
C) 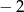 D)
D) 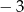
Suma odwrotności pierwiastków wielomianu 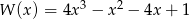 jest równa
jest równa
A) 4 B) 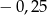 C) 6 D)
C) 6 D) 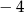
Rozwiązaniem równania 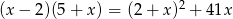 jest:
jest:
A) 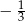 B)
B) 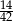 C)
C) 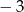 D)
D) 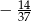
Rozwiązaniem równania 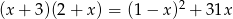 jest:
jest:
A) 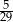 B)
B) 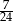 C)
C) 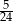 D)
D) 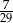
Ile rozwiązań ma równanie 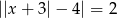 ?
?
A) 0 B) 2 C) 4 D) 6
Ile rozwiązań ma równanie 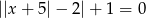 ?
?
A) 0 B) 2 C) 4 D) 6
Równanie 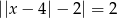 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Ile rozwiązań ma równanie 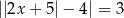 ?
?
A) 0 B) 1 C) 2 D) 4
Ile rozwiązań ma równanie 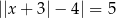 ?
?
A) 0 B) 2 C) 4 D) 6
Równanie 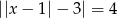 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Liczba pierwiastków wielomianu 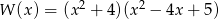 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba różnych miejsc zerowych wielomianu 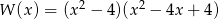 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 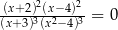
A) ma cztery różne rozwiązania: 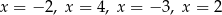 .
.
B) ma trzy różne rozwiązania: 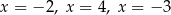 .
.
C) ma dwa różne rozwiązania: 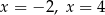 .
.
D) ma jedno rozwiązanie: 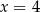 .
.
Liczba rozwiązań równania 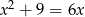 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Iloczyn pierwiastków równania 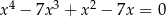 jest równy
jest równy
A) 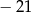 B) 14 C)
B) 14 C) 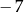 D) 0
D) 0
Para liczb 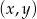 , która spełnia równanie
, która spełnia równanie 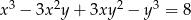 to
to
A) 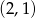 B)
B) 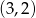 C)
C) 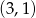 D)
D) 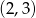
Jeśli 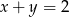 i
i 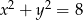 , to
, to 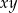 równa się
równa się
A) 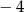 B) 2 C) 4 D)
B) 2 C) 4 D) 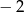
Równanie 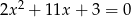
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Równanie 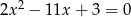
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Równanie 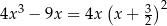 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Równanie 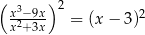
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Wśród miejsc zerowych wielomianu są liczby 0, 1, 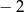 . Wielomian może mieć postać:
. Wielomian może mieć postać:
A) 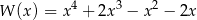 B)
B) 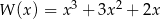
C) 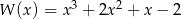 D)
D) 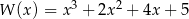
Dany jest wielomian 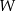 określony wzorem
określony wzorem 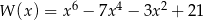 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 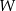 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 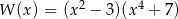 B)
B) 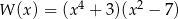
C) 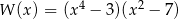 D)
D) 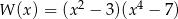
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 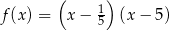 B)
B) 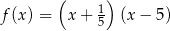
C) 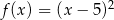 D)
D) 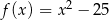
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 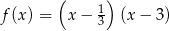 B)
B) 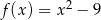
C) 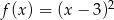 D)
D) 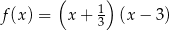
Pierwiastki trójmianu kwadratowego są liczbami odwrotnymi. Te warunki spełnia trójmian
A) 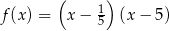 B)
B) 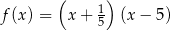
C) 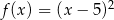 D)
D) 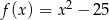
Rozwiązaniem równania 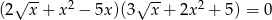 jest liczba
jest liczba
A) 1 B) 2 C) 4 D) 9
