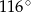Okrąg o środku 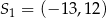 oraz okrąg o środku
oraz okrąg o środku 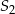 i promieniu 8 są styczne zewnętrznie w punkcie
i promieniu 8 są styczne zewnętrznie w punkcie 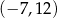 . Wtedy
. Wtedy
A) 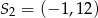 B)
B) 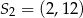 C)
C) 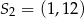 D)
D) 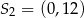
/Szkoła średnia/Zadania testowe/Geometria
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 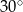 B)
B) 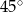 C)
C) 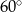 D)
D) 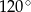
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od przekątnej podstawy tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 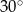 B)
B) 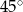 C)
C) 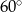 D)
D) 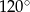
Długość przekątnej podstawy graniastosłupa prawidłowego czworokątnego jest równa długości jego wysokości. Z tego wynika, że miara kąta, jaki tworzy przekątna graniastosłupa z podstawą, jest równa
A) 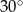 B)
B) 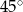 C)
C) 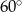 D)
D) 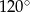
Przekątne trapezu 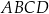 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 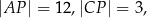
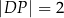 . Długość odcinka
. Długość odcinka 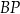 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątne trapezu 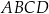 o podstawach
o podstawach 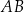 i
i 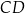 przecinają się w punkcie
przecinają się w punkcie 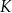 w ten sposób, że
w ten sposób, że 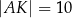 ,
, 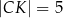 ,
, 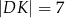 . Długość odcinka
. Długość odcinka 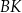 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
Przekątne trapezu 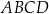 przecinają się w punkcie
przecinają się w punkcie 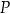 w ten sposób, że
w ten sposób, że 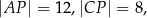
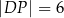 . Długość odcinka
. Długość odcinka 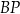 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątna równoległoboku dzieli go na dwa trójkąty równoramienne (zobacz rysunek).
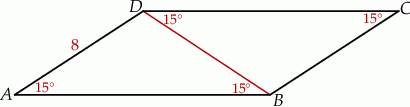
Pole tego równoległoboku jest równe
A) 16 B) 32 C) 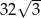 D)
D) 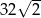
W trójkącie jeden z kątów jest o 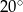 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 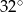 B)
B) 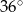 C)
C) 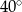 D)
D) 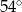
W trójkącie jeden z kątów jest o 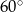 większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 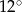 B)
B) 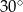 C)
C) 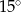 D)
D) 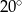
W trójkącie miary kątów są równe:  ,
, 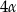 ,
, 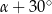 . Miara największego kąta tego trójkąta jest równa
. Miara największego kąta tego trójkąta jest równa
A) 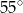 B)
B) 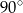 C)
C) 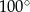 D)
D) 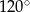
W trójkącie jeden z kątów jest o 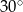 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 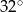 B)
B) 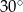 C)
C) 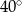 D)
D) 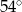
Jeden z kątów trójkąta jest trzy razy większy od drugiego. Miara trzeciego kąta jest o 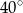 większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
A) 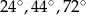 B)
B) 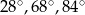 C)
C) 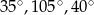 D)
D) 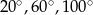
W równoległoboku 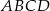 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 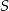 . Niech
. Niech 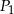 oznacza pole trójkąta
oznacza pole trójkąta 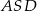 , natomiast
, natomiast 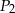 oznacza pole trójkąta
oznacza pole trójkąta 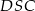 . Wówczas:
. Wówczas:
A) 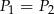 B)
B) 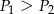 C)
C) 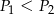 D)
D) 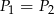 tylko wtedy, gdy
tylko wtedy, gdy 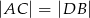
W równoległoboku 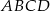 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 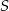 . Niech
. Niech 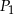 oznacza pole trójkąta
oznacza pole trójkąta 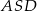 , natomiast
, natomiast 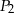 oznacza pole trójkąta
oznacza pole trójkąta 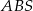 . Wówczas:
. Wówczas:
A) 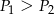 B)
B) 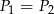 C)
C) 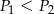 D)
D) 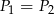 tylko wtedy, gdy
tylko wtedy, gdy 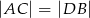
Cięciwy 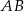 i
i 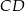 okręgu o środku
okręgu o środku 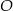 przecinają się w punkcie
przecinają się w punkcie 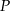 i tworzą trójkąty
i tworzą trójkąty 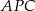 i
i 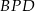 .
.
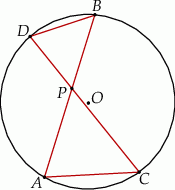
Trójkąty 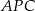 i
i 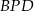 są
są
| A) podobne, | B) przystające, |
ponieważ trójkąty te mają równe
| 1) pola, | 2) miary kątów, | 3) długości boków, |
Punkty 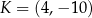 i
i 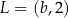 są końcami odcinka
są końcami odcinka 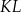 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 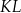 jest równa
jest równa 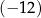 . Wynika stąd, że
. Wynika stąd, że
A) 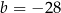 B)
B) 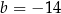 C)
C) 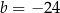 D)
D) 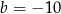
Pole powierzchni bocznej walca wynosi 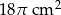 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 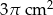 B)
B) 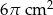 C)
C) 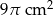 D)
D) 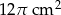
Odcinek 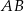 jest średnicą okręgu (rysunek).
jest średnicą okręgu (rysunek).
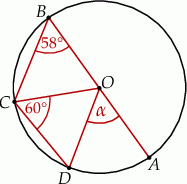
Miara kąta  jest równa
jest równa
A) 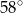 B)
B) 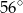 C)
C) 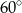 D)
D)