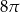Na płaszczyźnie, w kartezjańskim układzie współrzędnych 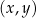 , dane są punkty
, dane są punkty 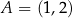 oraz
oraz 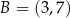 . Punkty
. Punkty 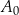 oraz
oraz 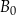 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów 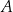 i
i 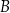 w symetrii środkowej o środku w punkcie
w symetrii środkowej o środku w punkcie 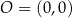 . Współczynnik kierunkowy prostej przechodzącej przez punkty
. Współczynnik kierunkowy prostej przechodzącej przez punkty 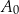 i
i 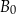 jest równy
jest równy
A)  B)
B) 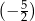 C)
C)  D)
D) 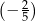
/Szkoła średnia/Zadania testowe/Geometria
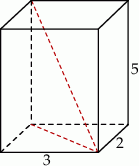
Przekątna prostopadłościanu o wymiarach 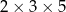 ma długość
ma długość
A) 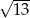 B)
B) 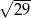 C)
C) 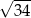 D)
D) 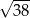
Przekątna prostopadłościanu o wymiarach 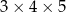 ma długość
ma długość
A) 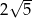 B)
B) 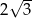 C)
C) 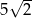 D)
D) 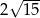
Przekątna prostopadłościanu o wymiarach 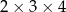 ma długość
ma długość
A) 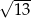 B)
B) 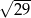 C) 5 D) 6
C) 5 D) 6
Okręgi o środkach 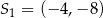 oraz
oraz 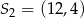 są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
A) 28 B) 24 C) 20 D) 16
Okrąg o środku 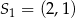 i promieniu
i promieniu  oraz okrąg o środku
oraz okrąg o środku 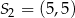 i promieniu 6 są styczne wewnętrznie. Wtedy
i promieniu 6 są styczne wewnętrznie. Wtedy
A) 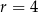 B)
B) 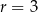 C)
C) 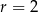 D)
D) 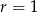
Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 4 cm, a wysokość jego ściany bocznej ma długość 5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 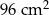 B)
B) 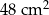 C)
C) 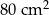 D)
D) 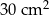
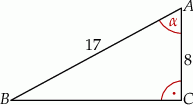
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
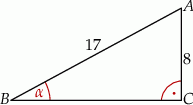
A) 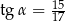 B)
B) 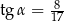 C)
C) 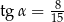 D)
D) 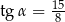
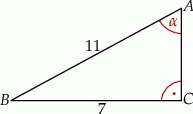
W trójkącie prostokątnym (patrz rysunek poniżej) tangens kąta ostrego  jest równy
jest równy
A) 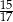 B)
B) 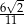 C)
C) 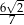 D)
D) 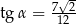
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
A) 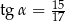 B)
B) 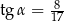 C)
C) 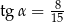 D)
D) 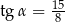
Punkt 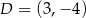 jest obrazem punktu
jest obrazem punktu 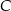 w symetrii względem punktu
w symetrii względem punktu 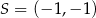 , a punkt
, a punkt 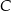 jest środkiem odcinka
jest środkiem odcinka 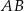 , gdzie
, gdzie 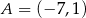 . Punkt
. Punkt 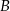 ma współrzędne
ma współrzędne
A) 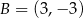 B)
B) 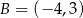 C)
C) 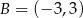 D)
D) 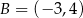
Punkt 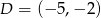 jest obrazem punktu
jest obrazem punktu  w symetrii względem punktu
w symetrii względem punktu 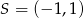 , a punkt
, a punkt 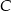 jest środkiem odcinka
jest środkiem odcinka 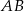 , gdzie
, gdzie 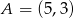 . Punkt
. Punkt 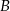 ma współrzędne
ma współrzędne
A) 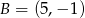 B)
B) 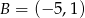 C)
C) 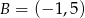 D)
D) 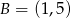
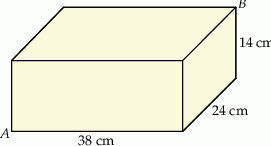
Pudełko w kształcie prostopadłościanu ma wymiary 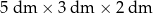 (zobacz rysunek).
(zobacz rysunek).
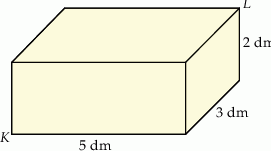
Przekątna 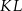 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 5,83 dm B) 6,16 dm C) 3,61 dm D) 5,39 dm
Bloczek betonowy fundamentowy ma kształt prostopadłościanu o wymiarach 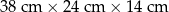 (zobacz rysunek).
(zobacz rysunek).
Przekątna 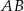 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 4,71 dm B) 4,49 dm C) 4,05 dm D) 4,7 dm
Pudełko w kształcie prostopadłościanu ma wymiary 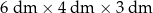 (zobacz rysunek).
(zobacz rysunek).
Przekątna 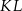 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 6,83 dm B) 6,16 dm C) 7,81 dm D) 5,39 dm
Punkt 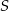 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 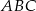 , w którym
, w którym 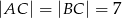 i
i 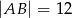 .
.
Wówczas miara  kąta
kąta  spełnia warunek
spełnia warunek
A) 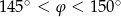 B)
B) 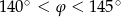 C)
C) 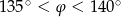 D)
D) 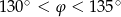
Punkt 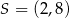 jest środkiem odcinka
jest środkiem odcinka 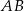 , gdzie
, gdzie 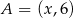 i
i 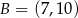 dla
dla  równego
równego
A) 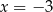 B)
B) 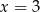 C)
C) 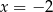 D)
D) 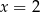
Dane są punkty 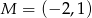 i
i 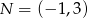 . Punkt
. Punkt 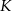 jest środkiem odcinka
jest środkiem odcinka 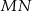 . Obrazem punktu
. Obrazem punktu 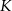 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 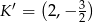 B)
B) 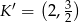 C)
C) 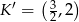 D)
D) 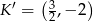
Dane są punkty 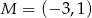 i
i 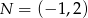 . Punkt
. Punkt 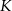 jest środkiem odcinka
jest środkiem odcinka 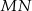 . Obrazem punktu
. Obrazem punktu 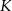 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 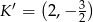 B)
B) 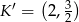 C)
C) 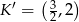 D)
D) 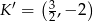
Jeśli 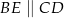 oraz
oraz 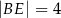 ,
, 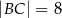 i
i 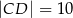 (patrz rysunek),
(patrz rysunek),
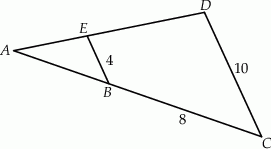
to długość odcinka 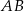 jest równa
jest równa
A) 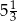 B)
B) 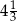 C)
C) 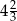 D)
D) 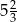
Proste o równaniach: 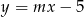 i
i 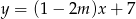 są równoległe, gdy
są równoległe, gdy
A) 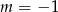 B)
B) 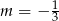 C)
C) 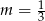 D)
D) 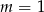
Proste o równaniach 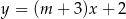 i
i 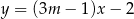 są równoległe, gdy
są równoległe, gdy
A) 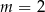 B)
B) 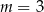 C)
C) 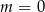 D)
D) 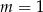
Proste o równaniach: 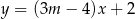 i
i 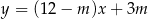 są równoległe, gdy
są równoległe, gdy
A) 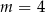 B)
B) 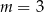 C)
C) 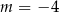 D)
D) 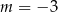
Proste o równaniach 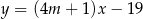 i
i 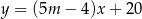 są równoległe, gdy
są równoległe, gdy
A) 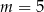 B)
B) 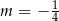 C)
C) 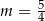 D)
D) 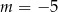
Prosta 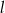 o równaniu
o równaniu 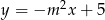 jest równoległa do prostej
jest równoległa do prostej 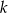 o równaniu
o równaniu 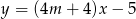 . Zatem
. Zatem
A) 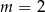 B)
B) 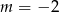 C)
C) 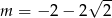 D)
D) 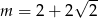
Proste 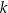 oraz
oraz 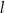 są określone równaniami
są określone równaniami
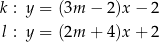
Proste 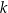 oraz
oraz 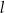 są równoległe, gdy liczba
są równoległe, gdy liczba 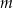 jest równa
jest równa
A) 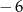 B)
B) 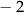 C) 2 D) 6
C) 2 D) 6
Proste o równaniach 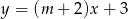 i
i 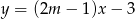 są równoległe, gdy
są równoległe, gdy
A) 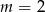 B)
B) 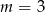 C)
C) 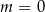 D)
D) 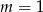
Proste 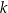 oraz
oraz 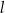 są określone równaniami
są określone równaniami
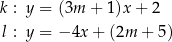
Proste 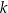 oraz
oraz 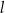 są równoległe, gdy liczba
są równoległe, gdy liczba 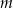 jest równa
jest równa
A) 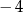 B)
B) 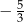 C)
C) 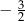 D)
D) 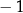
Prosta 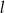 o równaniu
o równaniu 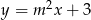 jest równoległa do prostej
jest równoległa do prostej 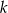 o równaniu
o równaniu 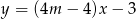 . Zatem
. Zatem
A) 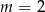 B)
B) 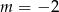 C)
C) 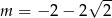 D)
D) 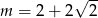
Proste o równaniach 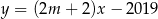 i
i 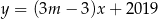 są równoległe, gdy
są równoległe, gdy
A) 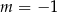 B)
B) 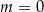 C)
C) 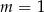 D)
D) 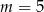
Podstawą ostrosłupa jest prostokąt 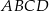 o bokach długości:
o bokach długości: 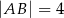 i
i 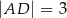 . Krawędź boczna
. Krawędź boczna 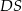 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
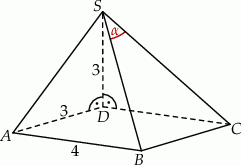
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 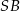 i
i 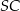 , to
, to
A) 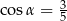 B)
B) 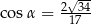 C)
C) 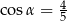 D)
D) 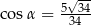
Podstawą ostrosłupa jest kwadrat  o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna  jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
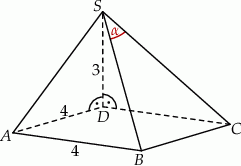
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 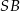 i
i 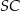 , to
, to
A) 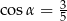 B)
B) 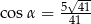 C)
C) 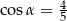 D)
D) 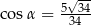
Punkty 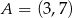 i
i 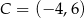 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 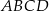 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 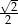 B)
B)  C)
C) 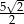 D) 5
D) 5
Punkty 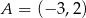 i
i 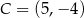 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu  . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 100 B) 50 C) 10 D) 5
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 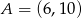 i
i 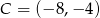 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 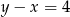 B)
B) 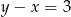 C)
C) 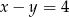 D)
D) 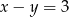
Obwód trójkąta 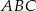 wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt
wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt 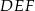 , którego obwód jest równy
, którego obwód jest równy
A) 6 cm B) 8 cm C) 12 cm D) 18 cm
Dany jest trójkąt o wierzchołkach 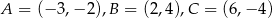 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 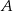 jest równa
jest równa
A) 4 B) 6 C) 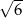 D)
D) 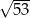
Dany jest trójkąt o wierzchołkach 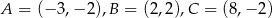 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 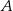 jest równa
jest równa
A) 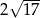 B)
B) 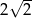 C)
C) 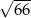 D)
D) 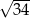
Dany jest trójkąt o wierzchołkach 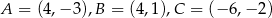 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 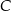 jest równa
jest równa
A) 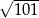 B)
B) 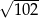 C)
C) 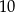 D)
D) 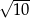
Dany jest trójkąt o wierzchołkach 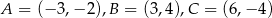 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 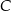 jest równa
jest równa
A) 11 B) 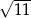 C)
C) 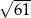 D)
D) 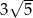
Na rysunku przedstawiono okrąg o środku 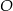 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 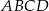 . Ramiona
. Ramiona 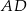 i
i 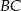 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 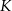 i
i 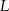 . Kąt wypukły
. Kąt wypukły 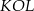 ma miarę
ma miarę 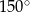 .
.
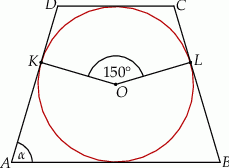
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 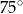 B)
B) 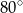 C)
C) 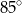 D)
D) 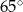
Na rysunku proste  i
i  są równoległe oraz
są równoległe oraz  . Wobec tego
. Wobec tego
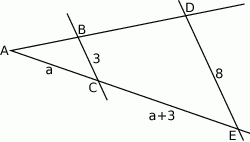
A) 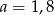 B)
B) 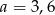 C)
C) 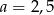 D)
D) 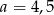
Na rysunku proste 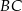 i
i 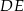 są równoległe oraz
są równoległe oraz 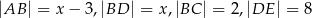 . Wobec tego
. Wobec tego  jest równe
jest równe
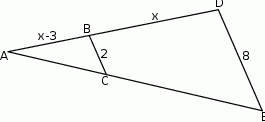
A) 3 B) 3,5 C) 4 D) 4,5
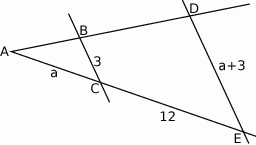
Na rysunku proste 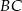 i
i 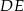 są równoległe oraz
są równoległe oraz 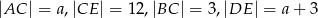 . Wobec tego
. Wobec tego
A) 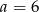 B)
B) 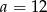 C)
C) 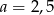 D)
D) 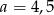
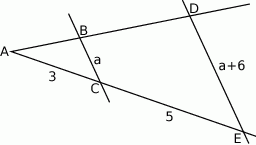
Na rysunku proste  i
i  są równoległe oraz
są równoległe oraz 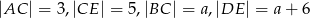 . Wobec tego
. Wobec tego
A) 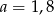 B)
B) 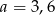 C)
C) 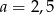 D)
D) 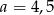
Kąty 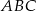 i
i 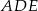 są równe oraz
są równe oraz 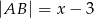 ,
, 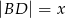 ,
, 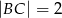 ,
, 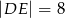 . Wobec tego
. Wobec tego  jest równe
jest równe
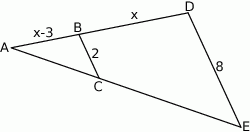
A) 3 B) 3,5 C) 4 D) 4,5
Objętość stożka o wysokości 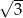 i kącie rozwarcia
i kącie rozwarcia  jest równa
jest równa
A) 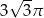 B)
B) 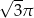 C)
C) 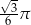 D)
D) 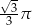
Kąt rozwarcia stożka ma miarę 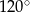 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 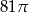 B)
B) 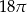 C)
C) 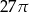 D)
D) 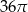
Kąt rozwarcia stożka ma miarę 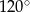 , a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
A) 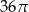 B)
B) 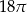 C)
C) 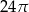 D)
D)