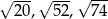Odcinek 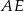 jest dwusieczną kąta
jest dwusieczną kąta 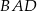 w równoległoboku
w równoległoboku 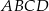 . Miara kąta
. Miara kąta 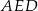 jest równa
jest równa 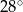 .
.
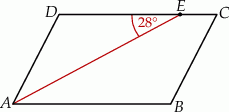
Miara kąta 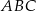 jest równa
jest równa
A) 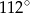 B)
B) 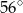 C)
C) 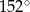 D)
D) 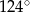
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinek 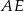 jest dwusieczną kąta
jest dwusieczną kąta 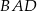 w równoległoboku
w równoległoboku 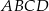 . Miara kąta
. Miara kąta 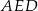 jest równa
jest równa 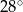 .
.

Miara kąta 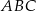 jest równa
jest równa
A) 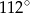 B)
B) 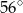 C)
C) 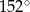 D)
D) 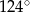
Prosta o równaniu 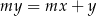 nie przecina prostej
nie przecina prostej 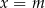 . Zatem
. Zatem
A) 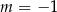 B)
B) 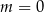 C)
C) 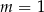 D)
D) 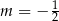
Krawędź podstawy graniastosłupa prawidłowego trójkątnego stanowi  wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
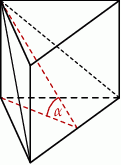
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 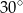 B)
B) 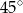 C)
C) 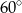 D)
D) 
Wysokość graniastosłupa prawidłowego trójkątnego jest równa połowie długości jego krawędzi podstawy. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
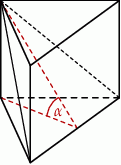
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 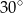 B)
B) 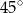 C)
C) 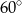 D)
D) 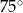
Punkty 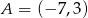 i
i 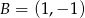 są wierzchołkami pięciokąta foremnego
są wierzchołkami pięciokąta foremnego 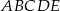 . Obwód tego pięciokąta jest równy
. Obwód tego pięciokąta jest równy
A) 50 B) 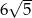 C) 60 D)
C) 60 D) 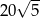
Punkty 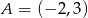 i
i 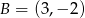 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 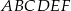 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 50 B) 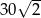 C) 300 D)
C) 300 D) 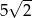
Podstawą ostrosłupa jest równoramienny trójkąt prostokątny 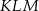 o przeciwprostokątnej długości
o przeciwprostokątnej długości 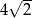 . Wysokością tego ostrosłupa jest krawędź
. Wysokością tego ostrosłupa jest krawędź 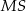 o długości 4 (zobacz rysunek).
o długości 4 (zobacz rysunek).
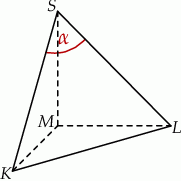
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 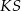 i
i 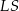 , spełnia warunek
, spełnia warunek
A) 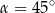 B)
B) 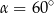 C)
C) 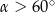 D)
D) 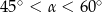
Dane są punkty 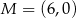 ,
, 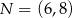 oraz
oraz 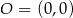 . Tangens kąta ostrego
. Tangens kąta ostrego 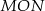 jest równy
jest równy
A) 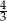 B)
B) 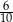 C)
C)  D)
D) 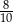
Dane są punkty 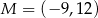 ,
, 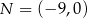 oraz
oraz 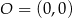 . Tangens kąta ostrego
. Tangens kąta ostrego 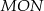 jest równy
jest równy
A) 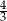 B)
B) 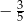 C)
C)  D)
D) 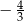
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 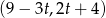 , gdzie
, gdzie 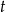 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 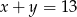 B)
B) 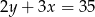 C)
C) 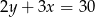 D)
D) 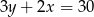
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 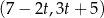 , gdzie
, gdzie 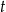 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 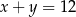 B)
B) 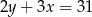 C)
C) 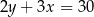 D)
D) 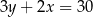
Proste prostopadłe 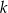 i
i 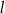 o równaniach
o równaniach 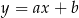 oraz
oraz 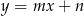 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 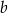 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 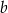 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 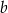 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 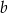 i
i  muszą być dodatnie
muszą być dodatnie
Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 20% B) wzrośnie o 40% C) wzrośnie o 44% D) wzrośnie dwukrotnie
Długość boku kwadratu 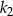 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 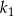 . Wówczas pole kwadratu
. Wówczas pole kwadratu 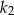 jest większe od pola kwadratu
jest większe od pola kwadratu 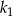 o
o
A) 10% B) 110% C) 21% D) 121%
Przekątna 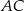 prostokąta
prostokąta 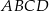 ma długość 70. Na boku
ma długość 70. Na boku 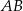 obrano punkt
obrano punkt 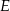 , na przekątnej
, na przekątnej 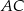 obrano punkt
obrano punkt 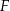 , a na boku
, a na boku 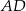 obrano punkt
obrano punkt 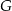 – tak, że czworokąt
– tak, że czworokąt 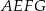 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 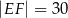 i
i 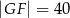 .
.
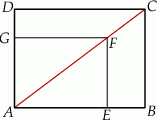
Obwód prostokąta 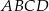 jest równy
jest równy
A) 158 B) 196 C) 336 D) 490
Przekątna 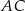 prostokąta
prostokąta 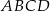 ma długość 104. Na boku
ma długość 104. Na boku 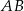 obrano punkt
obrano punkt 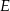 , na przekątnej
, na przekątnej 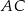 obrano punkt
obrano punkt 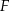 , a na boku
, a na boku 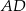 obrano punkt
obrano punkt 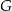 – tak, że czworokąt
– tak, że czworokąt 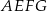 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 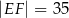 i
i 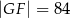 .
.
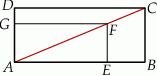
Obwód prostokąta 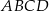 jest równy
jest równy
A) 272 B) 238 C) 221 D) 136
Liczba punktów wspólnych okręgu 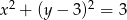 i prostej
i prostej 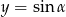 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych okręgu 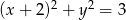 i prostej
i prostej 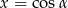 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych okręgu 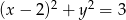 i prostej
i prostej 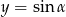 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Na bokach 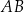 i
i 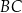 trójkąta
trójkąta 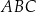 wybrano odpowiednio punkty
wybrano odpowiednio punkty 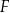 i
i 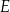 w ten sposób, że
w ten sposób, że 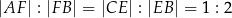 . Odcinki
. Odcinki 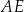 i
i 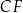 przecinają się w punkcie
przecinają się w punkcie 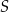 (zobacz rysunek).
(zobacz rysunek).
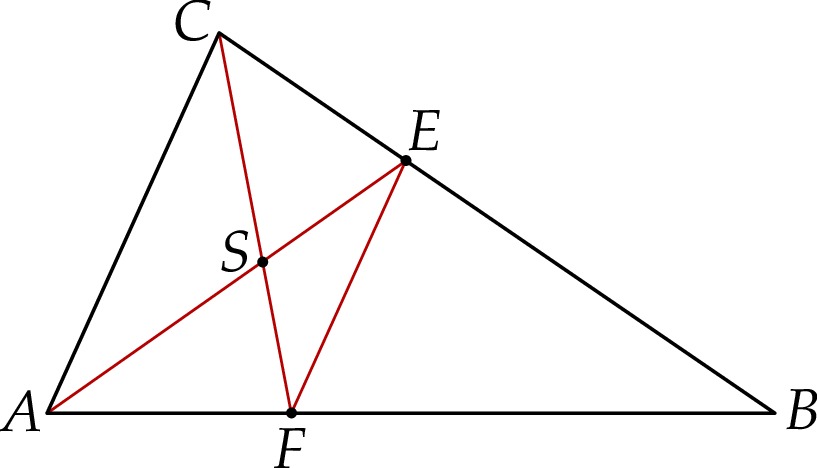
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 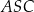 jest podobny do trójkąta jest podobny do trójkąta 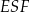 . . | P | F |
Pole trójkąta 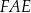 jest równe polu trójkąta jest równe polu trójkąta 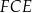 . . | P | F |
Dany jest trapez 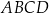 , w którym przekątna
, w którym przekątna 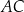 jest prostopadła do ramienia
jest prostopadła do ramienia 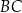 ,
, 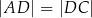 oraz
oraz 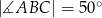 (zobacz rysunek).
(zobacz rysunek).
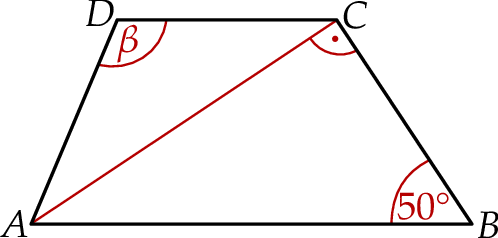
Stąd wynika, że
A) 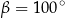 B)
B) 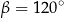 C)
C) 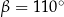 D)
D) 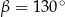
Dany jest trapez 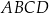 , w którym bok
, w którym bok 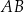 jest równoległy do boku
jest równoległy do boku 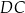 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 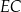 równoległy do boku
równoległy do boku 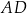 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 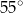 B)
B) 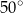 C)
C) 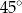 D)
D) 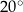
Dany jest trapez 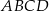 , w którym przekątna
, w którym przekątna 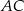 jest prostopadła do ramienia
jest prostopadła do ramienia 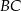 ,
, 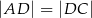 oraz
oraz 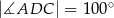 (zobacz rysunek).
(zobacz rysunek).
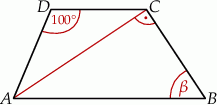
Stąd wynika, że
A) 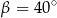 B)
B) 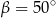 C)
C) 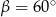 D)
D) 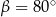
Kąt  jest kątem ostrym w trójkącie prostokątnym, a
jest kątem ostrym w trójkącie prostokątnym, a 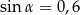 . Wówczas:
. Wówczas:
A) 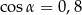 ,
, 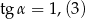 B)
B) 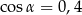 ,
, 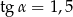
C) 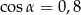 ,
, 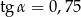 D)
D) 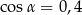 ,
, 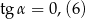
Prostymi równoległymi są wykresy funkcji liniowych:
A) 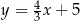 i
i 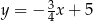 B)
B) 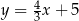 i
i 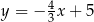
C) 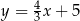 i
i 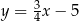 D)
D) 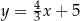 i
i 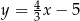
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 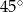 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 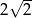 B)
B) 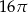 C)
C) 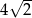 D)
D) 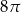
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 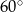 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 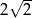 B)
B) 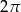 C)
C) 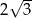 D) 2
D) 2
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 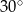 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 2 B) 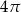 C)
C) 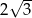 D)
D) 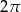
Powierzchnię boczną graniastosłupa prawidłowego czworokątnego o objętości 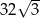 rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt
rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 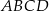 , w którym bok
, w którym bok 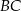 odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna 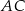 tworzy z bokiem
tworzy z bokiem 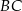 kąt o mierze
kąt o mierze 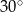 (zobacz rysunek).
(zobacz rysunek).
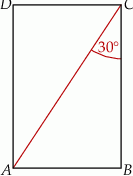
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 4 B) 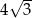 C)
C) 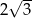 D) 2
D) 2
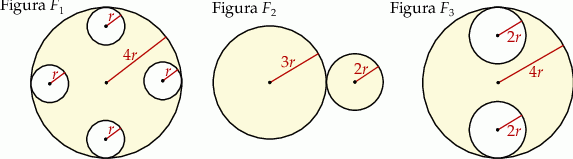
Na rysunku przedstawiono trzy figury. Figura 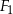 powstała z koła o promieniu
powstała z koła o promieniu 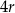 , z którego wycięto wnętrza czterech kół o promieniu
, z którego wycięto wnętrza czterech kół o promieniu  . Figura
. Figura 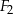 składa się z dwóch stycznych zewnętrznie kół o promieniach
składa się z dwóch stycznych zewnętrznie kół o promieniach 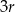 i
i 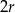 . Figura
. Figura 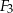 powstała z koła o promieniu
powstała z koła o promieniu 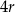 , z którego wycięto wnętrza dwóch kół o promieniu
, z którego wycięto wnętrza dwóch kół o promieniu 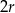 .
.
Jeżeli 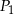 ,
, 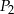 i
i 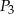 oznaczają pola figur odpowiednio
oznaczają pola figur odpowiednio 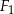 ,
, 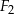 i
i 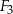 , to
, to
A) 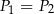 i
i 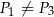 B)
B) 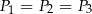
C) 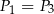 i
i 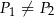 D)
D) 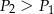
W każdym  –kącie wypukłym (
–kącie wypukłym (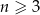 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 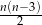 . Jeżeli graniastosłup prosty ma
. Jeżeli graniastosłup prosty ma 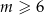 wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
A) 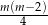 B)
B) 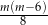 C)
C) 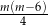 D)
D) 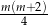
Liczby 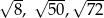 są długościami trójkąta
są długościami trójkąta 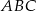 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 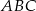 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 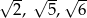 B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
Dany jest trójkąt o bokach długości 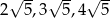 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 10, 15, 20 B) 20, 45, 80 C) 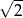 ,
, 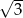 ,
, 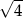 D)
D) 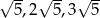
Liczby 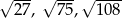 są długościami trójkąta
są długościami trójkąta 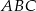 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 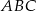 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 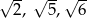 B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
Do trójkąta o bokach długości 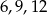 jest podobny trójkąt o bokach
jest podobny trójkąt o bokach
A) 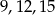 B)
B) 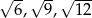 C)
C) 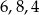 D)
D) 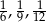
Dany jest trójkąt o bokach długości 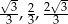 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 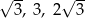 B)
B) 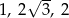 C)
C) 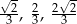 D)
D) 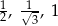
Boki trójkąta 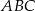 mają długości
mają długości 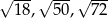 . Trójkątem do niego podobnym jest trójkąt o bokach
. Trójkątem do niego podobnym jest trójkąt o bokach
A) 3, 5, 6 B) 9, 25, 36 C) 18, 50, 72 D)