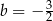W romb o boku 2 i kącie 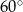 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy
A) 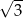 B)
B) 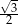 C)
C) 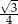 D)
D) 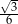
/Szkoła średnia/Zadania testowe/Geometria
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 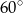 . Wysokość walca jest równa
. Wysokość walca jest równa 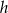 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 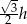 B)
B) 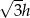 C)
C) 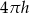 D)
D) 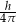
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 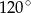 . Wysokość walca jest równa
. Wysokość walca jest równa 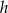 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 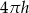 B)
B) 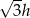 C)
C) 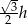 D)
D) 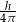
Pole powierzchni jednej ściany sześcianu jest równe 4. Objętość tego sześcianu jest równa
A) 6 B) 8 C) 24 D) 64
Pole powierzchni jednej ściany sześcianu jest równe 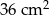 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 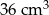 B)
B) 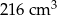 C)
C) 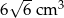 D)
D) 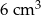
Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu jest równa
A) 9 B) 27 C) 54 D) 81
Ramię końcowe kąta 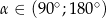 zawiera się w prostej
zawiera się w prostej 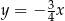 . Zatem
. Zatem
A) 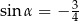 B)
B) 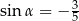 C)
C) 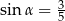 D)
D) 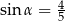
Punkty 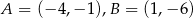 i
i 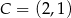 są trzema kolejnymi wierzchołkami rombu
są trzema kolejnymi wierzchołkami rombu 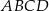 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 40 B) 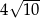 C) 80 D) 20
C) 80 D) 20
Punkty 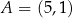 oraz
oraz 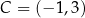 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 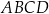 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 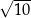 B)
B) 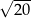 C)
C) 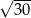 D)
D) 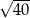
Punkty 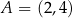 oraz
oraz 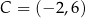 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 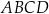 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 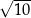 B)
B) 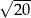 C)
C) 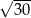 D)
D) 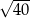
Punkty 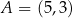 oraz
oraz 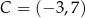 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 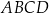 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 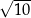 B)
B) 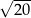 C)
C) 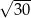 D)
D) 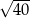
W kartezjańskim układzie współrzędnych 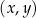 punkty
punkty 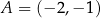 oraz
oraz 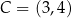 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 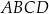 . Długość boku kwadratu
. Długość boku kwadratu 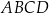 jest równa
jest równa
A) 5 B) 10 C) 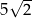 D)
D) 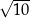
Punkt 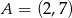 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 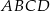 , a punkt
, a punkt 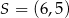 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 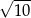 B)
B) 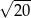 C)
C) 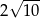 D)
D) 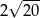
Punkt 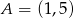 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 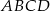 , a punkt
, a punkt 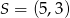 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 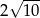 B)
B) 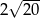 C)
C) 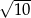 D)
D) 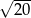
Dane są punkty 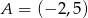 oraz
oraz 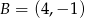 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 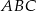 jest równy
jest równy
A) 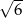 B)
B) 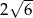 C)
C) 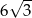 D)
D) 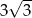
Punkty 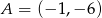 i
i 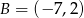 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 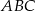 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 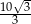 B)
B) 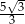 C)
C) 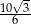 D)
D) 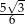
Punkty 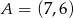 i
i 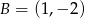 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 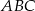 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 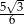 B)
B) 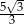 C)
C) 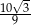 D)
D) 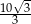
Prosta o równaniu 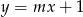 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 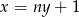 . Stąd wynika, że
. Stąd wynika, że
A) 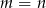 B)
B) 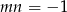 C)
C) 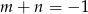 D)
D) 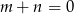
Prosta o równaniu 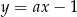 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 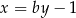 . Stąd wynika, że
. Stąd wynika, że
A) 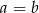 B)
B) 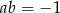 C)
C) 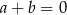 D)
D) 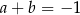
Przekątne deltoidu są zawarte w prostych o równaniach 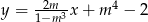 oraz
oraz 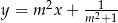 . Zatem
. Zatem
A) 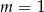 B)
B) 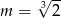 C)
C) 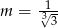 D)
D) 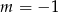
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 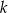 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 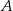 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 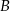 (zobacz rysunek).
(zobacz rysunek).
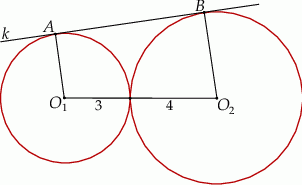
Długość odcinka 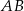 jest równa
jest równa
A) 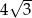 B) 7 C) 6 D)
B) 7 C) 6 D) 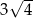
Punkt 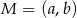 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 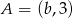 i
i 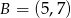 . Wówczas
. Wówczas
A) 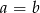 B)
B) 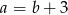 C)
C) 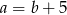 D)
D) 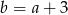
Punkt 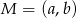 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 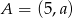 i
i 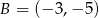 . Wówczas
. Wówczas
A) 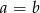 B)
B) 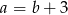 C)
C) 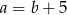 D)
D) 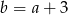
W układzie współrzędnych dane są punkty 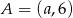 oraz
oraz 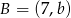 . Środkiem odcinka
. Środkiem odcinka 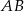 jest punkt
jest punkt 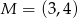 . Wynika stąd, że
. Wynika stąd, że
A) 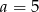 i
i 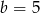 B)
B) 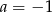 i
i 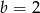 C)
C) 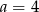 i
i 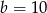 D)
D) 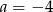 i
i 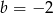
Jeżeli 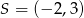 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 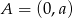 i
i 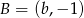 , to
, to
A) 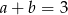 B)
B) 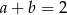 C)
C) 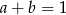 D)
D) 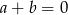
Środkiem odcinka o końcach 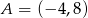 i
i 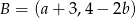 jest początek prostokątnego układu współrzędnych. Wówczas
jest początek prostokątnego układu współrzędnych. Wówczas
A) 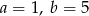 B)
B) 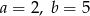 C)
C) 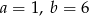 D)
D) 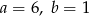
W układzie współrzędnych dane są punkty 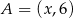 ,
, 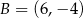 oraz
oraz 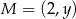 . Jeżeli punkt
. Jeżeli punkt 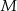 jest środkiem odcinka
jest środkiem odcinka 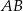 , to
, to
A) 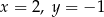 B)
B) 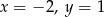 C)
C) 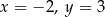 D)
D) 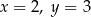
Punkt 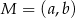 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 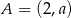 i
i 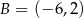 . Wówczas
. Wówczas
A) 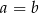 B)
B) 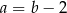 C)
C) 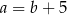 D)
D) 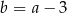
W układzie współrzędnych dane są punkty 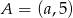 oraz
oraz 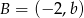 . Środkiem odcinka
. Środkiem odcinka 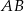 jest punkt
jest punkt 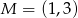 . Wynika stąd, że
. Wynika stąd, że
A) 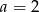 i
i 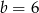 B)
B) 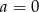 i
i 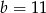 C)
C) 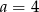 i
i 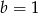 D)
D) 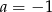 i
i 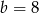
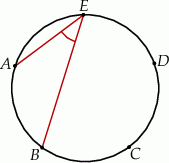
Punkty 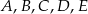 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 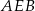 jest równa
jest równa
A) 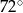 B)
B) 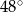 C)
C) 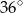 D)
D) 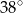
Punkty 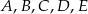 leżące na okręgu o środku
leżące na okręgu o środku 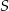 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 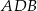 jest równa
jest równa
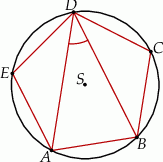
A) 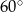 B)
B) 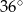 C)
C) 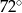 D)
D) 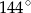
Punkty 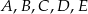 okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 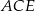 jest równa
jest równa
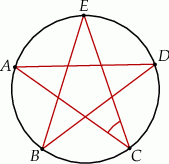
A) 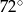 B)
B) 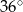 C)
C) 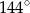 D)
D) 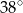
W trójkącie równoramiennym 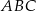 dane są
dane są 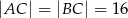 oraz
oraz 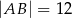 . Odcinek
. Odcinek 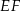 jest równoległy do podstawy
jest równoległy do podstawy 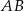 oraz
oraz 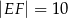 . Długość odcinka
. Długość odcinka 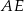 jest równa
jest równa
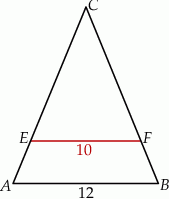
A) 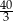 B)
B)  C)
C) 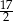 D)
D) 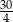
W trójkącie równoramiennym 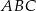 dane są
dane są 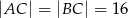 oraz
oraz 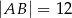 . Odcinek
. Odcinek 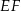 jest równoległy do podstawy
jest równoległy do podstawy 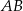 oraz
oraz 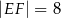 . Długość odcinka
. Długość odcinka 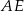 jest równa
jest równa
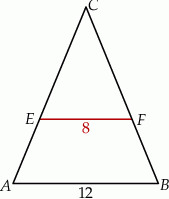
A) 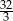 B)
B)  C)
C) 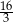 D)
D) 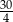
Punkty 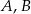 i
i 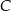 leżą na okręgu o środku
leżą na okręgu o środku 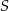 (zobacz rysunek).
(zobacz rysunek).
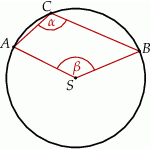
Miary  i
i 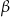 zaznaczonych kątów
zaznaczonych kątów 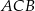 i
i 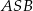 spełniają warunek
spełniają warunek 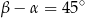 . Wynika stąd, że
. Wynika stąd, że
A) 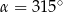 B)
B) 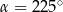 C)
C) 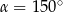 D)
D) 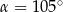
Suma długości wszystkich przekątnych sześcianu jest równa 24. Pole powierzchni całkowitej tego sześcianu jest równe
A) 144 B) 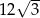 C) 36 D) 72
C) 36 D) 72
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 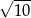 B)
B) 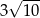 C)
C) 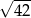 D)
D) 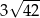
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy krótsza od krawędzi podstawy, jest równe 60. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 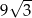 B)
B) 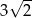 C)
C) 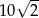 D)
D) 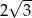
Środkiem okręgu jest punkt 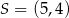 . Do okręgu należy punkt
. Do okręgu należy punkt 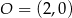 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 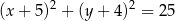 B)
B) 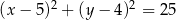
C) 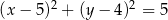 D)
D) 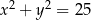
Środkiem okręgu jest punkt 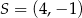 . Do okręgu należy punkt
. Do okręgu należy punkt 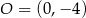 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 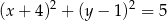 B)
B) 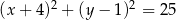
C) 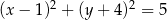 D)
D) 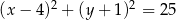
Środkiem okręgu jest punkt 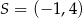 . Do okręgu należy punkt
. Do okręgu należy punkt 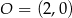 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 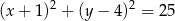 B)
B) 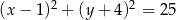
C) 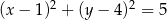 D)
D) 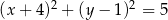
Punkt 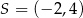 jest środkiem okręgu. Na okręgu leży punkt
jest środkiem okręgu. Na okręgu leży punkt 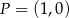 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 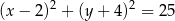 B)
B) 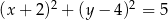
C) 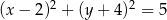 D)
D) 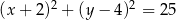
Dane są dwie proste równoległe 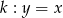 oraz
oraz 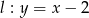 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 1,5 C) 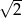 D) 1
D) 1
Odległość między prostymi 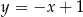 i
i 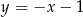 jest równa
jest równa
A) 2 B) 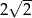 C) 1 D)
C) 1 D) 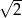
Dane są dwie proste równoległe 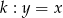 oraz
oraz 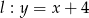 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 4 B) 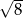 C)
C) 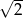 D) 3
D) 3
Dane są dwie proste równoległe 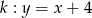 oraz
oraz 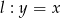 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 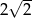 C)
C) 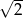 D) 4
D) 4
Punkty 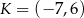 i
i 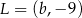 są końcami odcinka
są końcami odcinka 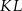 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 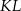 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 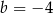 B)
B) 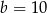 C)
C) 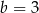 D)
D)