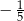Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,49 B) 5,9 C) 5,85 D) 5,5
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,49 B) 5,9 C) 5,85 D) 5,5
Z przeciwległych wierzchołków kwadratu o boku 1 zatoczono koła o promieniu 1. Pole części wspólnej tych kół jest równe
A) 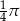 B)
B) 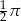 C)
C) 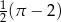 D)
D) 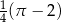
Z przeciwległych wierzchołków kwadratu o boku 2 zatoczono koła o promieniu 2. Pole części wspólnej tych kół jest równe
A) 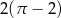 B)
B) 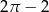 C)
C) 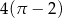 D)
D) 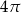
Cięciwa dzieli okrąg na dwa łuki w stosunku 5:7. Miara kąta wpisanego opartego na krótszym łuku okręgu jest równa
A) 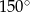 B)
B) 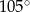 C)
C) 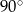 D)
D) 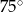
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 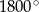 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 12
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 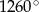 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 7 B) 9 C) 10 D) 11
Jeżeli suma kątów wewnętrznych wielokąta foremnego jest równa 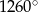 to wielokąt ten ma wierzchołków:
to wielokąt ten ma wierzchołków:
A) 8 B) 10 C) 7 D) 9
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 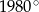 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 7 B) 9 C) 13 D) 12
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 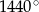 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 8
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Promień okręgu opisanego na tym trójkącie jest równy
A) 12 B) 8,5 C) 6,5 D) 5
Na trójkącie prostokątnym, którego przyprostokątne mają długości 12 i 9, opisano okrąg. Promień tego okręgu jest równy
A) 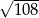 B)
B) 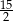 C) 15 D)
C) 15 D) 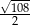
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C) 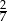 D)
D) 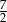
Dla jakiej wartości parametru 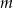 punkt przecięcia prostych
punkt przecięcia prostych 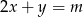 i
i 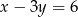 należy do osi
należy do osi 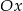 ?
?
A) dla 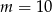 B) dla
B) dla 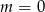 C) dla
C) dla 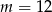 D) dla
D) dla 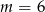
Proste o równaniach 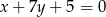 i
i 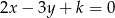 przecinają się na osi
przecinają się na osi 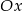 . Zatem parametr
. Zatem parametr 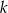 jest równy
jest równy
A) 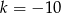 B)
B) 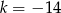 C)
C) 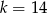 D)
D) 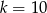
W trójkącie prostokątnym o polu 15 najkrótszy bok ma długość 3. Obwód tego trójkąta jest równy
A) 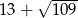 B)
B) 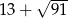 C)
C) 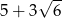 D)
D) 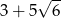
Środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
A) dwusiecznych kątów trójkąta B) środkowych trójkąta
C) wysokości trójkąta D) symetralnych boków trójkąta
Dla dowolnego trójkąta prawdziwe jest zdanie
A) Środek okręgu wpisanego w trójkąt to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się dwusiecznych kątów trójkąta.
D) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta
Dany jest stożek o objętości 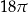 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 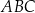 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 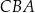 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 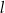 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 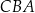 jest równy 2.
jest równy 2.
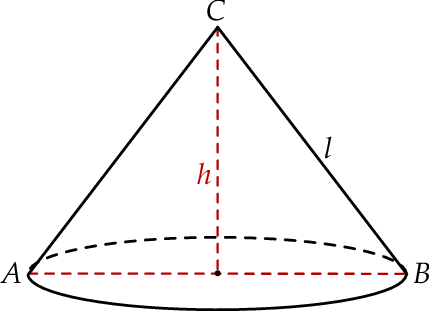
Wynika stąd, że wysokość 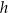 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Obrazem odcinka 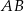 o końcach w punktach
o końcach w punktach 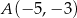 ,
, 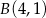 w symetrii względem osi
w symetrii względem osi 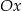 , jest odcinek
, jest odcinek 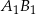 o końcach w punktach
o końcach w punktach
A) 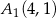 ,
, 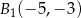 B)
B) 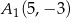 ,
, 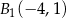
C) 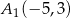 ,
, 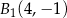 D)
D) 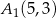 ,
, 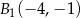
Przekątna kwadratu jest o 2 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 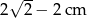 B)
B) 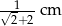 C)
C) 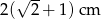 D)
D) 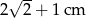
Przekątna kwadratu jest o 3 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 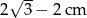 B)
B) 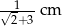 C)
C) 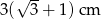 D)
D) 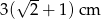
Przekątna kwadratu jest o 4 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 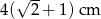 B)
B) 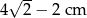 C)
C) 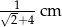 D)
D) 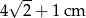
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 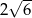 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 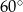 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 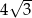 B) 6 C) 12 D) 4
B) 6 C) 12 D) 4
Przekątna graniastosłupa prawidłowego czworokątnego ma długość równą 16 i jest nachylona do płaszczyzny podstawy pod kątem 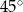 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 8 B) 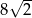 C)
C) 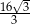 D)
D) 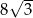
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 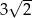 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 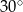 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 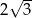 B) 6 C)
B) 6 C) 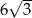 D) 4
D) 4
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36, a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 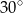 . Wysokość tego graniastosłupa jest równa
. Wysokość tego graniastosłupa jest równa
A) 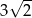 B)
B) 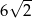 C)
C) 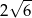 D)
D) 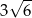
Przekątna graniastosłupa prawidłowego czworokątnego o długości równej 10 cm jest nachylona do płaszczyzny podstawy pod kątem 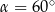 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 5 cm B) 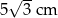 C)
C) 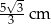 D)
D) 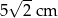
Dany jest trójkąt prostokątny o kątach ostrych  i
i 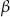 , w którym
, w którym 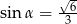 . Wtedy
. Wtedy
A) 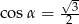 B)
B) 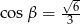 C)
C) 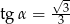 D)
D) 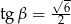
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
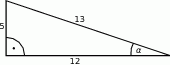
A) 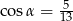 B)
B) 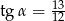 C)
C) 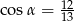 D)
D) 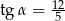
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
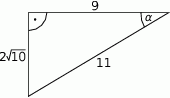
A) 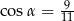 B)
B) 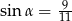 C)
C) 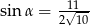 D)
D) 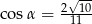
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
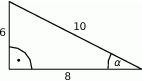
A) 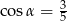 B)
B) 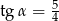 C)
C) 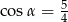 D)
D) 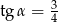
Jeżeli punkty 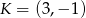 i
i 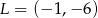 są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
A) 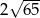 B)
B) 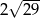 C)
C) 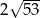 D)
D) 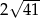
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 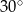 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 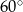 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 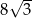 B)
B) 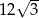 C)
C) 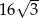 D)
D) 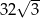
Punkty 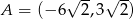 i
i 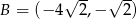 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 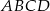 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 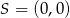 . Środek boku
. Środek boku 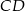 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 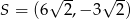 B)
B) 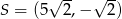 C)
C) 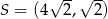 D)
D) 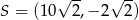
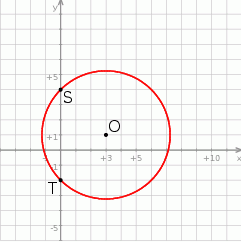
Okrąg przedstawiony na rysunku ma środek w punkcie 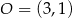 i przechodzi przez punkty
i przechodzi przez punkty 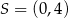 i
i 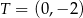 . Okrąg ten jest opisany przez równanie
. Okrąg ten jest opisany przez równanie
A) 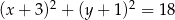 B)
B) 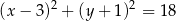
C) 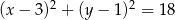 D)
D) 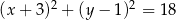
W graniastosłupie prawidłowym sześciokątnym 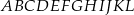 wierzchołki
wierzchołki 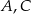 i
i 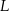 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
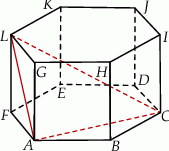
Cosinus największego kąta trójkąta 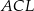 jest równy
jest równy
A)  B)
B) 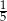 C) 0 D)
C) 0 D)