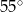Środek  okręgu o równaniu
okręgu o równaniu 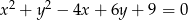 ma współrzędne
ma współrzędne
A) 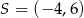 B)
B) 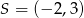 C)
C) 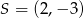 D)
D) 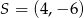
/Szkoła średnia/Zadania testowe/Geometria
Środkiem okręgu o równaniu 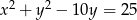 jest punkt
jest punkt
A) 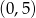 B)
B) 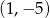 C)
C) 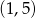 D)
D) 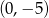
Środek okręgu o równaniu 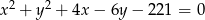 ma współrzędne
ma współrzędne
A) 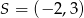 B)
B) 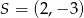 C)
C) 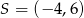 D)
D) 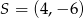
Środek 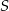 okręgu o równaniu
okręgu o równaniu 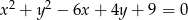 ma współrzędne
ma współrzędne
A) 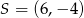 B)
B) 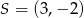 C)
C) 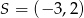 D)
D) 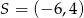
Środek 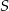 okręgu o równaniu
okręgu o równaniu 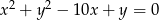 ma współrzędne
ma współrzędne
A) 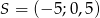 B)
B) 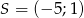 C)
C) 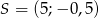 D)
D) 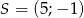
Środek 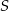 okręgu o równaniu
okręgu o równaniu 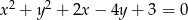 ma współrzędne
ma współrzędne
A) 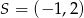 B)
B) 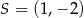 C)
C) 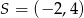 D)
D) 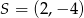
Środek 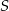 okręgu o równaniu
okręgu o równaniu 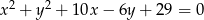 ma współrzędne
ma współrzędne
A) 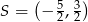 B)
B) 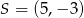 C)
C) 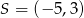 D)
D) 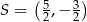
Punkt 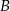 jest symetryczny do punktu
jest symetryczny do punktu 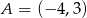 względem osi
względem osi 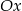 układu współrzędnych, a punkt
układu współrzędnych, a punkt 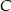 jest symetryczny do punktu
jest symetryczny do punktu 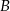 względem osi
względem osi 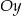 . Zatem trójkąt
. Zatem trójkąt 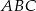 jest
jest
A) równoboczny
B) prostokątny i równoramienny
C) prostokątny i żaden z jego kątów nie jest równy 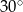
D) prostokątny z kątem ostrym równym 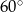
W kwadracie 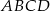 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 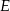 i
i 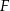 na bokach
na bokach 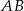 i
i 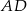 w ten sposób, że odcinek
w ten sposób, że odcinek 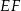 jest równoległy do przekątnej
jest równoległy do przekątnej 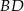 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
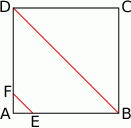
Długość odcinka 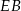 jest równa
jest równa
A) 12 B) 15 C) 14 D) 16
W trójkącie prostokątnym przeciwprostokątna ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 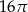 B)
B) 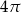 C)
C) 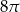 D)
D) 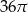
Pole koła opisanego na trójkącie prostokątnym o bokach długości 10, 24, 26 jest równe
A) 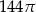 B)
B) 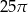 C)
C) 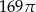 D)
D) 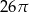
Wzór funkcji liniowej, której wykresem jest prosta nachylona do osi 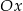 pod kątem o mierze
pod kątem o mierze 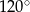 i przechodzi przez punkt
i przechodzi przez punkt 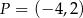 jest postaci
jest postaci
A) 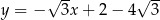 B)
B) 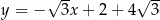
C) 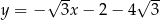 D)
D) 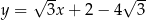
Wykres funkcji liniowej 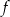 jest nachylony do osi
jest nachylony do osi 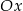 pod kątem
pod kątem 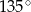 . Wiadomo, że
. Wiadomo, że 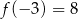 . Funkcja liniowa
. Funkcja liniowa 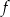 jest określona wzorem
jest określona wzorem
A) 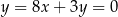 B)
B) 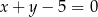
C) 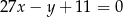 D)
D) 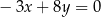
Objętość sześcianu jest równa 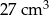 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 18 cm B) 36 cm C) 24 cm D) 12 cm
Objętość sześcianu jest równa 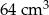 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 48 cm B) 36 cm C) 24 cm D) 64 cm
Na rysunku przedstawiono okrąg wpisany w trójkąt.
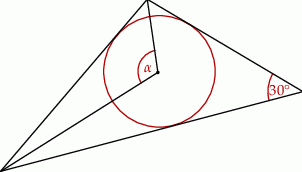
Miara kąta  jest równa
jest równa
A) 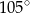 B)
B) 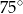 C)
C) 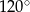 D)
D) 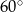
Okrąg o środku w punkcie 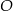 jest wpisany w trójkąt
jest wpisany w trójkąt 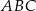 . Wiadomo, że
. Wiadomo, że 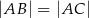 i
i 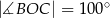 (zobacz rysunek).
(zobacz rysunek).
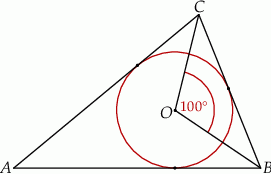
Miara kąta 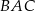 jest równa
jest równa
A) 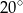 B)
B) 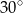 C)
C) 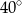 D)
D) 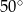
Okrąg o środku w punkcie 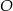 jest wpisany w trójkąt
jest wpisany w trójkąt 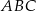 . Wiadomo, że
. Wiadomo, że 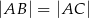 i
i 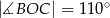 (zobacz rysunek).
(zobacz rysunek).
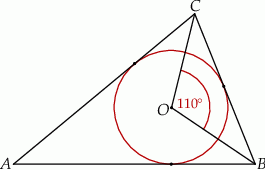
Miara kąta  jest równa
jest równa
A)  B)
B)  C)
C) 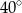 D)
D) 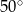
Odległość między środkami okręgów o równaniach 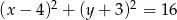 oraz
oraz 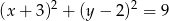 jest równa
jest równa
A) 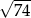 B)
B) 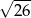 C)
C) 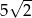 D)
D) 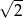
Proste o równaniach 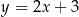 oraz
oraz 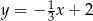
A) są równoległe i różne B) są prostopadłe
C) przecinają się pod kątem innym niż prosty D) pokrywają się
Równania 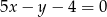 oraz
oraz 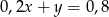 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 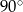
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 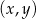 , dane są:
, dane są:
– prosta 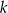 o równaniu
o równaniu 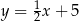
– prosta 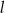 o równaniu
o równaniu 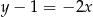 .
.
Proste 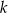 i
i 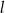
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 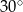 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 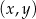 , dane są:
, dane są:
– prosta 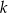 o równaniu
o równaniu 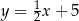
– prosta 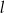 o równaniu
o równaniu 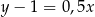 .
.
Proste 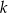 i
i 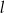
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 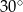 .
.
Proste o równaniach 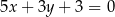 oraz
oraz 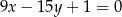
A) są równoległe i różne B) są prostopadłe
C) przecinają się pod kątem innym niż prosty D) pokrywają się
Proste o równaniach 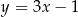 oraz
oraz 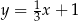
A) pokrywają się B) przecinają się pod kątem innym niż prosty
C) są prostopadłe D) są równoległe i różne
Równania 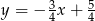 oraz
oraz 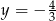 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 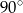 .
.
B) pokrywające się
C) przecinające się pod kątem różnym od 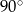 .
.
D) równoległe i różne.
Równania 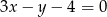 oraz
oraz 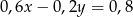 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 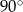
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 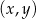 , dane są proste
, dane są proste 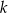 oraz
oraz 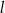 o równaniach
o równaniach
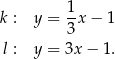
Proste 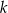 oraz
oraz 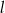
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 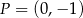 . D) pokrywają się.
. D) pokrywają się.
Równania 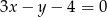 oraz
oraz 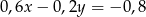 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 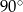
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 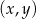 , dane są proste
, dane są proste 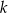 oraz
oraz 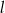 o równaniach
o równaniach
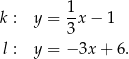
Proste  oraz
oraz 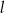
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 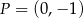 . D) pokrywają się.
. D) pokrywają się.
Równania 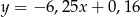 oraz
oraz 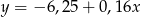 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 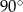 .
.
B) pokrywające się.
C) przecinające się pod kątem różnym od 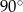 .
.
D) równoległe i różne.
W trójkącie prostokątnym miary kątów ostrych są równe  i
i 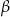 . Wartość wyrażenia
. Wartość wyrażenia 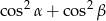 jest równa
jest równa
A) 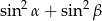 B)
B) 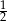 C)
C) 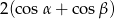 D)
D) 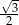
Punkty 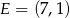 i
i 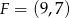 to środki boków, odpowiednio
to środki boków, odpowiednio 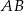 i
i 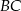 kwadratu
kwadratu 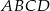 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 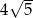 B) 10 C)
B) 10 C) 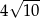 D) 20
D) 20
Punkty 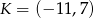 i
i 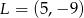 to środki boków, odpowiednio
to środki boków, odpowiednio 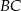 i
i 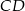 kwadratu
kwadratu 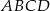 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 32 B) 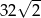 C)
C) 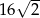 D) 16
D) 16
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 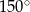 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 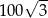 D)
D) 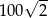
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 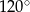 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 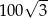 D)
D) 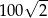
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 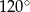 jest równe
jest równe
A) 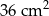 B)
B) 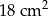 C)
C) 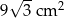 D)
D) 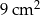
Ramię trójkąta równoramiennego 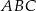 ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 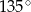 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 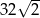 B)
B) 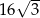 C) 32 D)
C) 32 D) 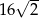
Wierzchołki trójkąta 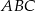 mają współrzędne
mają współrzędne 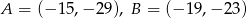 i
i 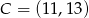 . Bok
. Bok 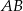 trójkąta
trójkąta  ma długość
ma długość
A) 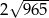 B)
B) 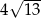 C)
C) 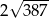 D)
D) 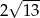
Wysokość rombu o boku długości 6 i kącie ostrym 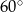 jest równa
jest równa
A) 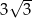 B) 3 C)
B) 3 C) 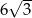 D) 6
D) 6
Wysokość rombu o boku długości 8 i kącie ostrym 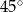 jest równa
jest równa
A) 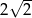 B) 4 C)
B) 4 C) 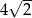 D) 8
D) 8
Dany jest sześciokąt foremny 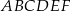 o polu równym
o polu równym 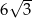 (zobacz rysunek).
(zobacz rysunek).
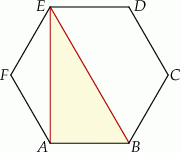
Pole trójkąta 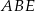 jest równe
jest równe
A) 6 B) 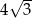 C)
C) 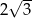 D) 4
D) 4
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 9 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) osiemnastokąt. D) dziesięciokąt.
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 10 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) jedenastokąt. D) dziesięciokąt.
Na trójkącie  opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie  (zobacz rysunek obok).
(zobacz rysunek obok).
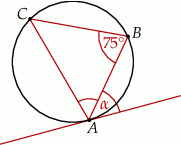
Jeżeli 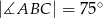 i kąt dopisany
i kąt dopisany  jest równy
jest równy 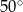 , to kąt
, to kąt 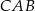 ma miarę:
ma miarę:
A) 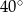 B)
B) 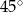 C)
C) 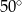 D)
D) 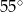
Czworokąt  jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 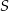 . Bok
. Bok 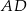 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 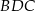 jest równa
jest równa 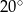 (zobacz rysunek).
(zobacz rysunek).
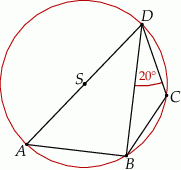
Wtedy miara kąta 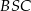 jest równa
jest równa
A) 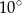 B)
B) 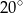 C)
C) 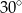 D)
D) 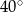
Czworokąt 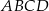 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 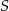 . Bok
. Bok 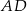 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 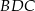 jest równa
jest równa 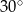 (zobacz rysunek).
(zobacz rysunek).
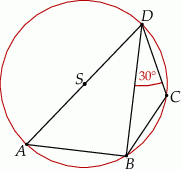
Wtedy miara kąta 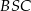 jest równa
jest równa
A) 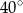 B)
B) 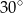 C)
C) 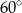 D)
D) 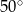
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 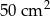 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 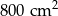 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 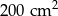 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
W trójkącie 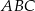 , w którym
, w którym 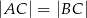 , na boku
, na boku 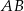 wybrano punkt
wybrano punkt 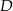 taki, że
taki, że 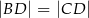 oraz
oraz 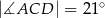 (zobacz rysunek).
(zobacz rysunek).
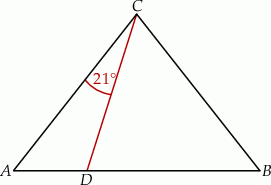
Wynika stąd, że kąt 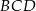 ma miarę
ma miarę
A) 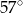 B)
B) 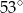 C)
C) 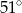 D)
D) 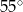
Dany jest trójkąt równoramienny 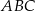 , w którym
, w którym 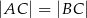 . Na podstawie
. Na podstawie 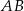 tego trójkąta leży punkt
tego trójkąta leży punkt 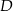 , taki że
, taki że 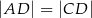 ,
, 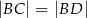 oraz
oraz 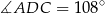 (zobacz rysunek).
(zobacz rysunek).
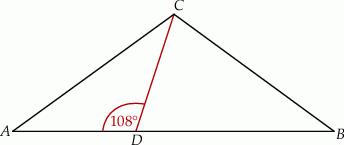
Wynika stąd, że kąt 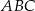 ma miarę
ma miarę
A) 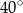 B)
B) 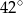 C)
C) 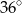 D)
D) 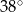
Dany jest trójkąt równoramienny 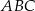 , w którym
, w którym 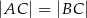 . Na podstawie
. Na podstawie 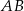 tego trójkąta leży punkt
tego trójkąta leży punkt 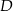 , taki że
, taki że 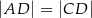 ,
, 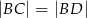 oraz
oraz 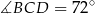 (zobacz rysunek).
(zobacz rysunek).
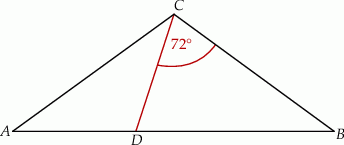
Wynika stąd, że kąt 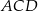 ma miarę
ma miarę
A) 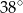 B)
B) 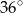 C)
C) 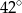 D)
D) 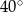
W trójkącie 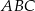 , w którym
, w którym 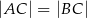 , na boku
, na boku 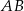 wybrano punkt
wybrano punkt 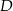 taki, że
taki, że 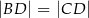 oraz
oraz 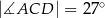 (zobacz rysunek).
(zobacz rysunek).
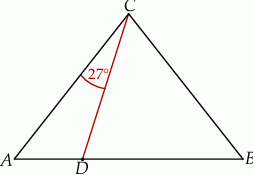
Wynika stąd, że kąt 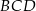 ma miarę
ma miarę
A) 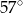 B)
B) 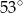 C)
C) 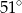 D)
D)