Punkty 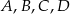 leżą na okręgu o środku
leżą na okręgu o środku 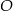 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 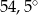 B)
B) 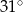 C)
C) 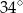 D)
D) 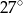
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 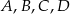 leżą na okręgu o środku
leżą na okręgu o środku 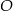 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa

A) 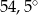 B)
B) 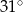 C)
C) 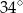 D)
D) 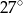
Punkty 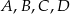 leżą na okręgu o środku
leżą na okręgu o środku 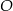 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
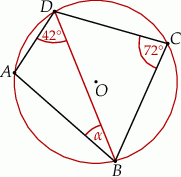
A) 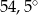 B)
B) 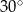 C)
C) 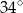 D)
D) 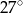
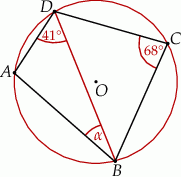
Punkty 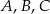 i
i 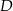 leżą na okręgu o środku
leżą na okręgu o środku 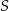 . Miary kątów
. Miary kątów 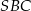 ,
, 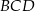 ,
, 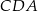 są równe odpowiednio:
są równe odpowiednio: 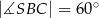 ,
, 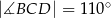 ,
, 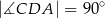 (zobacz rysunek).
(zobacz rysunek).
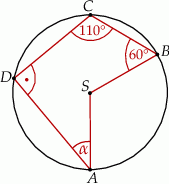
Wynika stąd, że miara  kąta
kąta 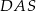 jest równa
jest równa
A) 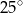 B)
B) 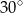 C)
C) 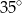 D)
D) 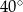
Punkty 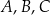 i
i 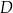 leżą na okręgu o środku
leżą na okręgu o środku 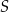 . Miary kątów
. Miary kątów 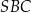 ,
, 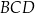 ,
, 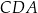 są równe odpowiednio:
są równe odpowiednio: 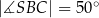 ,
, 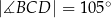 ,
, 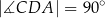 (zobacz rysunek).
(zobacz rysunek).
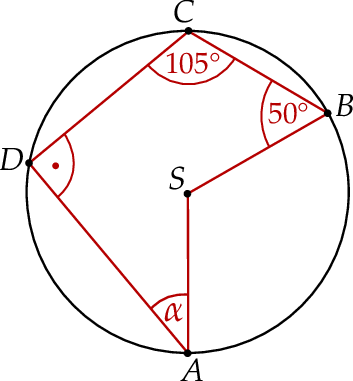
Wynika stąd, że miara  kąta
kąta 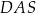 jest równa
jest równa
A) 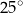 B)
B) 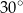 C)
C) 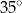 D)
D) 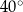
Punkty 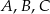 i
i 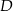 leżą na okręgu o środku
leżą na okręgu o środku 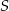 . Miary kątów
. Miary kątów 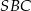 ,
, 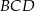 ,
, 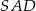 są równe odpowiednio:
są równe odpowiednio: 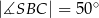 ,
, 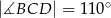 ,
, 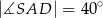 (zobacz rysunek).
(zobacz rysunek).
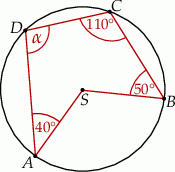
Wynika stąd, że miara  kąta
kąta 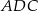 jest równa
jest równa
A) 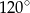 B)
B) 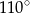 C)
C) 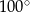 D)
D) 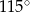
Wskaż równanie okręgu opisanego na trójkącie 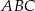 o wierzchołkach
o wierzchołkach 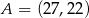 ,
, 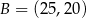 ,
, 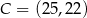
A) 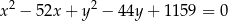 B)
B) 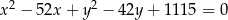
C) 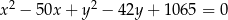 D)
D) 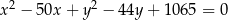
Przekątna graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 2 razy dłuższa od krawędzi podstawy, jest równa 6. Wynika stąd, że objętość tego graniastosłupa jest równa
A) 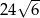 B)
B) 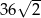 C)
C) 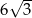 D)
D) 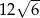
Trójkąt prostokątny ma boki długości 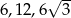 i kąty ostre
i kąty ostre 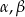 . Kąt
. Kąt 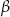 leży naprzeciw boku długości
leży naprzeciw boku długości 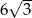 . Zatem
. Zatem
A) 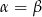 B)
B) 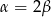 C)
C) 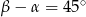 D)
D) 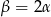
Trójkąt prostokątny ma boki długości 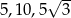 i kąty ostre
i kąty ostre 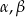 . Kąt
. Kąt 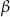 leży naprzeciw boku długości
leży naprzeciw boku długości 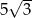 . Zatem
. Zatem
A) 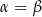 B)
B) 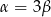 C)
C) 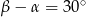 D)
D) 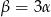
Trójkąt prostokątny ma boki długości 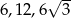 i kąty ostre
i kąty ostre 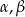 . Kąt
. Kąt 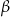 leży naprzeciw boku długości 6. Zatem
leży naprzeciw boku długości 6. Zatem
A) 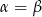 B)
B) 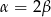 C)
C) 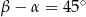 D)
D) 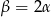
Okrąg o średnicy 6 jest styczny do osi 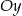 , a oś
, a oś 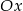 jest jego osią symetrii. Środek tego okręgu ma współrzędne
jest jego osią symetrii. Środek tego okręgu ma współrzędne
A) 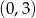 B)
B) 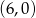 C)
C) 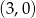 D)
D) 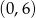
Punkty 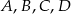 dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego 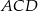 jest równa
jest równa
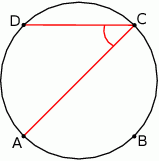
A) 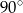 B)
B) 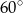 C)
C) 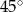 D)
D) 
Punkt 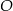 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 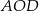 ma miarę
ma miarę
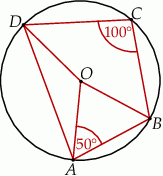
A) 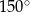 B)
B) 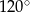 C)
C) 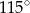 D)
D) 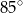
Punkt 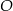 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 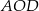 ma miarę
ma miarę
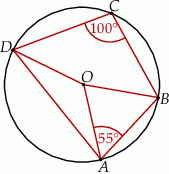
A) 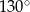 B)
B) 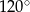 C)
C) 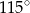 D)
D) 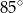
Punkty 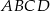 leżą na okręgu o środku
leżą na okręgu o środku 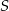 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 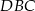 jest równa
jest równa
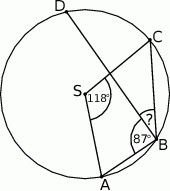
A) 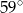 B)
B) 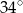 C)
C) 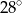 D)
D) 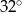
Punkt 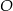 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
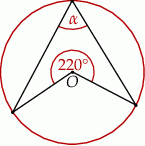
A) 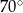 B)
B) 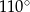 C)
C) 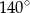 D)
D) 
Punkt 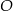 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
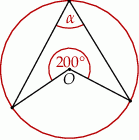
A) 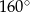 B)
B) 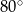 C)
C) 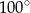 D)
D) 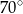
Miara kąta  (patrz rysunek obok) jest równa
(patrz rysunek obok) jest równa
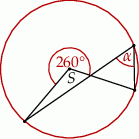
A) 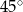 B)
B) 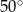 C)
C) 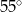 D)
D) 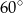
Środek 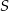 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 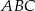 należy do boku
należy do boku 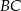 . Suma miar kątów
. Suma miar kątów 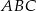 i
i 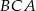 trójkąta
trójkąta 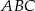 jest równa
jest równa
A) 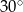 B)
B) 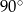 C)
C) 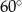 D)
D) 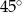
Środek 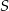 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 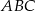 należy do boku
należy do boku 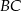 . Miara kąta
. Miara kąta 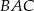 trójkąta
trójkąta 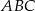 jest równa
jest równa
A) 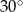 B)
B) 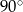 C)
C) 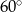 D)
D) 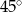
Punkty 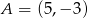 ,
, 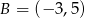 ,
, 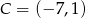 i
i 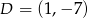 są wierzchołkami prostokąta
są wierzchołkami prostokąta 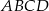 . Pole tego prostokąta jest równe
. Pole tego prostokąta jest równe
A) 16 B) 32 C) 64 D) 96
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 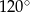 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 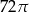 B)
B) 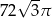 C)
C) 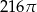 D)
D) 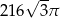
Na podstawie 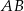 i ramieniu
i ramieniu 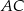 trójkąta równoramiennego
trójkąta równoramiennego 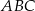 dane są punkty
dane są punkty 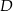 i
i 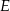 takie, że
takie, że 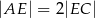 i
i 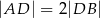 . Punkty
. Punkty 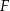 i
i 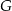 leżą na ramieniu
leżą na ramieniu 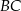 tak, że odcinki
tak, że odcinki 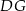 i
i 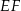 są prostopadłe do prostej
są prostopadłe do prostej 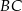 (zobacz rysunek).
(zobacz rysunek).
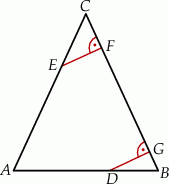
Pole trójkąta 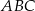 jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów 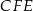 i
i 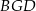 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Punkty 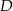 i
i 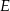 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 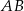 i ramienia
i ramienia 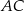 trójkąta równoramiennego
trójkąta równoramiennego 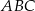 . Punkty
. Punkty 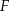 i
i 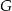 leżą na ramieniu
leżą na ramieniu 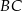 tak, że odcinki
tak, że odcinki 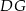 i
i 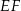 są prostopadłe do prostej
są prostopadłe do prostej 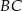 (zobacz rysunek).
(zobacz rysunek).
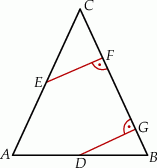
Pole trójkąta 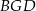 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 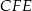 jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 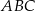 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Punkty 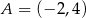 i
i 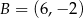 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 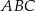 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 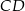 tego trójkąta przecina prostą
tego trójkąta przecina prostą 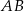 w punkcie
w punkcie
A) 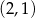 B)
B) 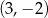 C)
C) 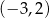 D)
D) 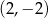
Punkty 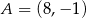 i
i 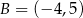 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 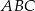 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 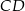 tego trójkąta przecina prostą
tego trójkąta przecina prostą 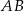 w punkcie
w punkcie
A) 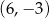 B)
B) 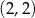 C)
C) 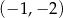 D)
D) 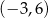
Punkt 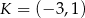 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 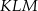 , w którym
, w którym 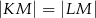 . Odcinek
. Odcinek 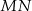 jest wysokością trójkąta i
jest wysokością trójkąta i 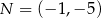 . Zatem
. Zatem
A) 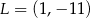 B)
B) 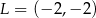 C)
C) 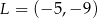 D)
D) 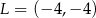
Punkt 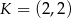 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 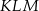 , w którym
, w którym 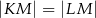 . Odcinek
. Odcinek 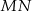 jest wysokością trójkąta i
jest wysokością trójkąta i 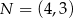 . Zatem
. Zatem
A) 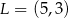 B)
B) 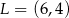 C)
C) 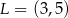 D)
D) 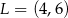
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 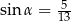 . Bok
. Bok 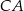 tego trójkąta ma długość:
tego trójkąta ma długość:
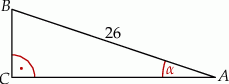
A) 10 B) 24 C) 12 D) 5
Dany jest trójkąt prostokątny o bokach długości 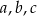 .
.
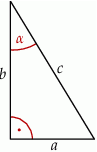
Jeżeli 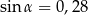 oraz
oraz 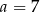 , to
, to
A) 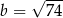 B)
B) 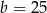 C)
C) 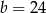 D)
D) 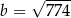
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 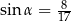 . Bok
. Bok 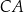 tego trójkąta ma długość:
tego trójkąta ma długość:
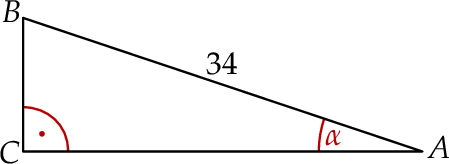
A) 30 B) 8 C) 16 D) 24
Jeśli 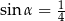 , to długość przyprostokątnej
, to długość przyprostokątnej 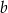 danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
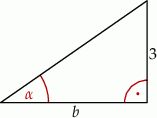
A) 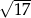 B)
B) 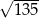 C)
C) 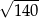 D)
D) 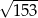
Jeśli 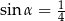 , to długość przyprostokątnej
, to długość przyprostokątnej  danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
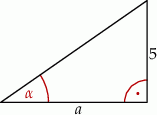
A) 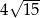 B)
B) 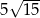 C)
C) 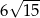 D)
D) 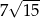
Miara kąta między bokiem 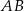 równoległoboku
równoległoboku 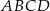 , a przekątną
, a przekątną 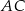 jest równa
jest równa 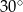 . Długość przekątnej
. Długość przekątnej 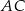 jest równa 5, a długość boku
jest równa 5, a długość boku 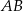 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 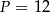 B)
B) 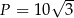 C)
C) 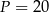 D)
D) 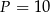
Obwód trójkąta 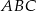 wynosi 28 cm, a jego pole jest równe
wynosi 28 cm, a jego pole jest równe 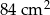 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 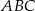 jest równy
jest równy
A) 3 cm B) 6 cm C) 4 cm D) 7 cm
Punkt 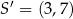 jest obrazem punktu
jest obrazem punktu 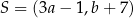 w symetrii osiowej względem osi
w symetrii osiowej względem osi 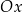 układu współrzędnych, gdy
układu współrzędnych, gdy
A) 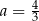 oraz
oraz 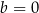 B)
B) 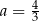 oraz
oraz 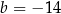
C) 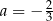 oraz
oraz 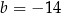 D)
D) 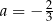 oraz
oraz 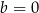
Trójkąt, w którym stosunek długości boków jest równy 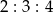 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Trójkąt, w którym stosunek długości boków jest równy 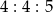 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Powierzchnia sześcianu wynosi 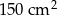 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Powierzchnia sześcianu wynosi 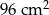 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Pole powierzchni całkowitej sześcianu jest równe 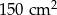 . Długość krawędzi tego sześcianu jest równa
. Długość krawędzi tego sześcianu jest równa
A) 3,5 cm B) 4 cm C) 4,5 cm D) 5 cm
Powierzchnia sześcianu wynosi 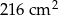 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 3 cm B) 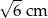 C) 12 cm D) 6 cm
C) 12 cm D) 6 cm
