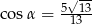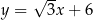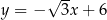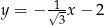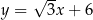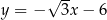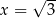Dany jest trójkąt prostokątny o długościach boków 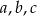 , gdzie
, gdzie 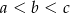 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 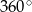 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
A) 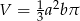 B)
B) 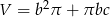 C)
C) 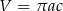 D)
D) 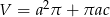
/Szkoła średnia/Zadania testowe/Geometria
Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 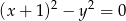 , jest
, jest
A) parabolą B) prostą C) okręgiem D) sumą dwóch prostych
Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 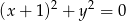 , jest
, jest
A) parabolą B) punktem C) okręgiem D) sumą dwóch prostych
Miara kąta wpisanego opartego na  okręgu wynosi:
okręgu wynosi:
A) 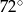 B)
B) 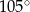 C)
C) 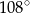 D)
D) 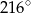
Miara kąta wpisanego opartego na łuku długości 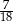 długości całego okręgu wynosi
długości całego okręgu wynosi
A) 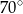 B)
B) 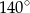 C)
C) 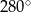 D)
D) 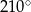
Kąt wpisany oparty jest na łuku, którego długość jest równa 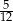 długości okręgu. Miara tego kąta wynosi
długości okręgu. Miara tego kąta wynosi
A) 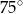 B)
B) 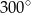 C)
C) 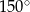 D)
D) 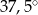
Jaką miarę ma kąt wpisany oparty na 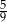 łuku okręgu?
łuku okręgu?
A) 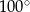 B)
B) 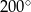 C)
C) 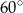 D)
D) 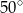
Miara kąta wpisanego opartego na  długości okręgu jest równa
długości okręgu jest równa
A) 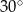 B)
B) 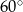 C)
C) 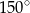 D)
D) 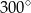
Dane są dwa okręgi: okrąg o środku w punkcie  i promieniu 5 oraz okrąg o środku w punkcie
i promieniu 5 oraz okrąg o środku w punkcie 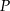 i promieniu 3. Odcinek
i promieniu 3. Odcinek 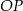 ma długość 16. Prosta
ma długość 16. Prosta 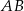 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 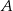 i
i 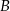 . Ponadto prosta
. Ponadto prosta 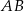 przecina odcinek
przecina odcinek 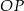 w punkcie
w punkcie 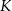 (zobacz rysunek).
(zobacz rysunek).
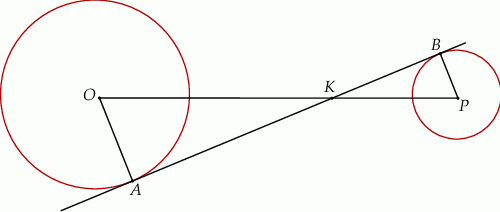
Wtedy
A) 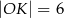 B)
B) 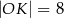 C)
C) 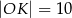 D)
D) 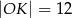
Dane są dwa okręgi: okrąg o środku w punkcie 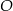 i promieniu 4 oraz okrąg o środku w punkcie
i promieniu 4 oraz okrąg o środku w punkcie 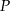 i promieniu 6. Odcinek
i promieniu 6. Odcinek 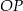 ma długość 25. Prosta
ma długość 25. Prosta 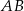 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 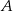 i
i 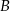 . Ponadto prosta
. Ponadto prosta 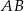 przecina odcinek
przecina odcinek 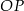 w punkcie
w punkcie 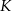 (zobacz rysunek).
(zobacz rysunek).
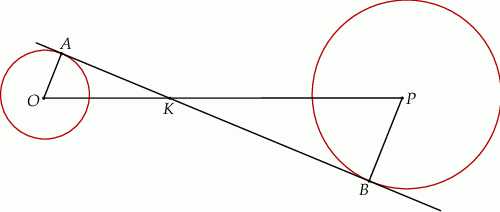
Wtedy
A) 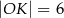 B)
B) 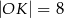 C)
C) 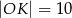 D)
D) 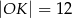
Jeśli promień podstawy stożka zwiększymy trzykrotnie, a wysokość zmniejszymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zwiększy się sześciokrotnie
Jeśli promień podstawy stożka zmniejszymy trzykrotnie, a wysokość zwiększymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zmniejszy się trzykrotnie
Jeśli promień podstawy stożka zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to objętość stożka
A) zwiększy się dwukrotnie B) nie zmieni się
C) zwiększy się czterokrotnie D) zmniejszy się czterokrotnie
Końce odcinka 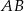 o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
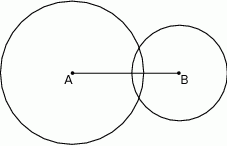
Punkt 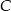 leży na odcinku
leży na odcinku 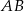 i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku
i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku 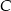 ma długość
ma długość
A) 6,5 B) 7,5 C) 8,5 D) 9,5
W kartezjańskim układzie współrzędnych 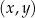 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 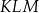 . Trójkąt
. Trójkąt 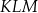 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 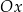 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 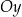 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
W kartezjańskim układzie współrzędnych 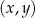 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 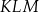 . Trójkąt
. Trójkąt 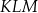 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 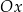 jest osią symetrii tego trójkąta. jest osią symetrii tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | jedna z tych prostych jest równoległa do osi 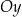 . . |
Jeżeli  jest kątem wewnętrznym trójkąta
jest kątem wewnętrznym trójkąta 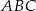 i
i 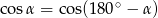 , to trójkąt
, to trójkąt 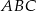 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 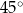 (zobacz rysunek).
(zobacz rysunek).
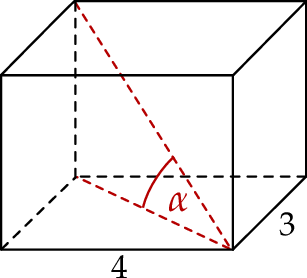
Wysokość graniastosłupa jest równa
A) 5 B) 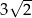 C)
C) 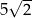 D)
D) 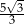
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki tworzą dwie przekątne tego graniastosłupa, jest równy
, jaki tworzą dwie przekątne tego graniastosłupa, jest równy 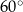 (zobacz rysunek).
(zobacz rysunek).
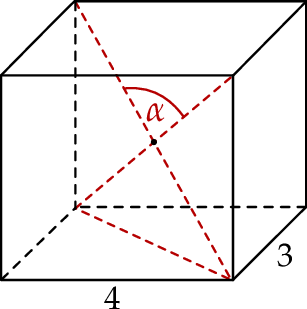
Wysokość graniastosłupa jest równa
A) 10 B) 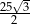 C)
C) 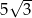 D)
D) 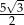
Graniastosłup prosty ma pole powierzchni całkowitej równe 94, a w jego podstawie jest prostokąt o bokach długości 3 i 4 (zobacz rysunek).
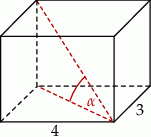
Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
A) 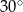 B)
B) 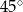 C)
C) 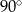 D)
D) 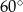
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 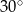 (zobacz rysunek).
(zobacz rysunek).
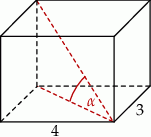
Wysokość graniastosłupa jest równa
A) 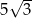 B)
B) 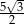 C)
C) 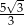 D)
D) 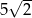
Miara kąta  wynosi
wynosi
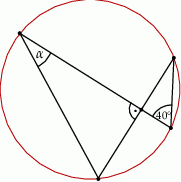
A) 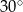 B)
B) 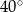 C)
C) 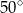 D)
D) 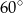
Miara kąta  wynosi
wynosi
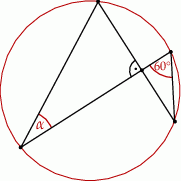
A) 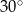 B)
B) 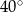 C)
C) 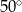 D)
D) 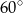
Miara kąta  wynosi
wynosi
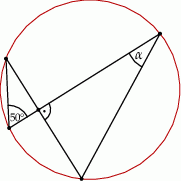
A) 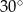 B)
B) 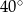 C)
C) 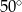 D)
D) 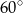
Kąt  na rysunku obok ma miarę
na rysunku obok ma miarę
A) 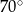 B)
B) 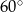 C)
C) 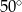 D)
D) 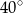
Punkty 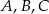 i
i 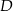 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 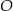 . Cięciwy
. Cięciwy 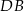 i
i 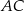 przecinają się w punkcie
przecinają się w punkcie 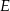 ,
, 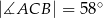 oraz
oraz 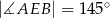 (zobacz rysunek).
(zobacz rysunek).
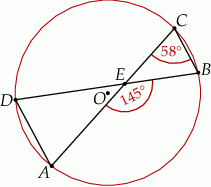
Miara kąta 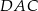 jest równa
jest równa
A) 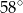 B)
B) 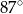 C)
C) 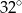 D)
D) 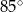
Punkty 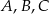 i
i 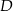 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 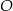 . Cięciwy
. Cięciwy 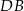 i
i 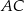 przecinają się w punkcie
przecinają się w punkcie 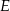 ,
, 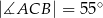 oraz
oraz 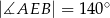 (zobacz rysunek).
(zobacz rysunek).
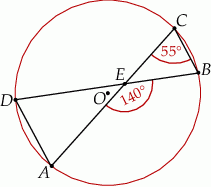
Miara kąta 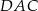 jest równa
jest równa
A) 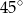 B)
B) 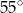 C)
C) 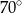 D)
D) 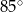
Objętość kuli o promieniu 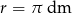 jest równa
jest równa
A) 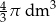 B)
B) 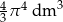 C)
C) 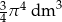 D)
D) 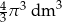
Objętość kuli o promieniu 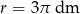 jest równa
jest równa
A) 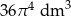 B)
B) 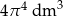 C)
C) 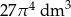 D)
D) 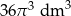
Prosta 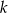 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 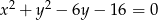 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 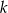 jest równa
jest równa
A) 9 B) 4 C) 25 D) 5
Prosta  jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 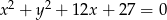 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 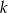 jest równa
jest równa
A) 9 B) 3 C) 25 D) 5
Pole trójkąta 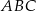 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
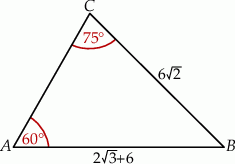
A) 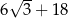 B)
B) 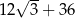 C)
C) 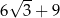 D)
D) 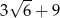
W układzie współrzędnych dane są punkty 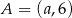 oraz
oraz 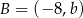 . Punkt
. Punkt 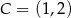 jest takim punktem odcinka
jest takim punktem odcinka  , że
, że 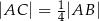 . Wynika stąd, że
. Wynika stąd, że
A) 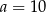 i
i 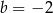 B)
B) 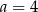 i
i 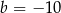 C)
C) 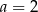 i
i 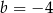 D)
D) 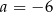 i
i 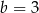
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 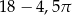 B)
B) 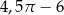 C)
C) 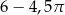 D)
D) 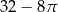
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 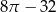 B)
B) 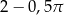 C)
C) 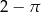 D)
D) 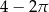
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 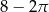 B)
B) 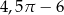 C)
C) 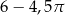 D)
D) 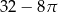
Pole trójkąta 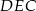 wynosi
wynosi 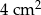 . Wiadomo, że
. Wiadomo, że 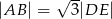 oraz
oraz 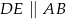 . Zatem pole trójkąta
. Zatem pole trójkąta 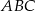 jest równe
jest równe
A) 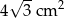 B)
B) 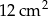 C)
C) 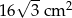 D)
D) 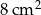
Prosta 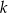 przecina oś
przecina oś 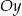 układu współrzędnych w punkcie
układu współrzędnych w punkcie 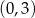 i jest prostopadła do prostej o równaniu
i jest prostopadła do prostej o równaniu 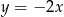 . Wówczas prosta
. Wówczas prosta 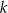 przecina oś
przecina oś 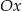 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 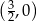 B)
B) 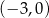 C)
C) 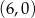 D)
D) 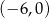
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 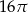 B)
B) 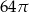 C)
C) 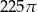 D)
D) 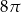
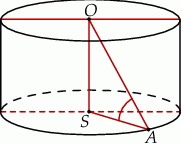
Promień 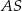 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 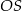 tego walca. Sinus kąta
tego walca. Sinus kąta 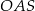 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 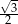 B)
B) 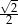 C)
C) 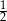 D) 1
D) 1
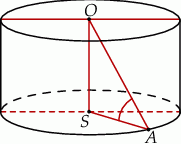
Promień 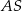 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 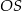 tego walca. Tangens kąta
tego walca. Tangens kąta  (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 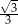 B)
B) 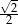 C)
C) 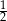 D) 1
D) 1
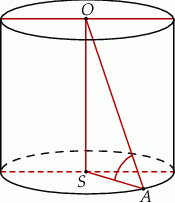
Promień 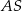 podstawy walca jest równy połowie wysokości
podstawy walca jest równy połowie wysokości 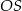 tego walca. Sinus kąta
tego walca. Sinus kąta 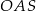 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 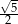 B)
B) 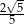 C)
C) 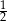 D) 1
D) 1
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 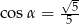 B)
B) 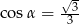 C)
C) 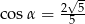 D)
D) 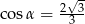
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 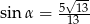 B)
B) 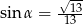 C)
C) 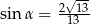 D)
D) 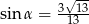
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 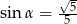 B)
B) 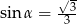 C)
C) 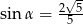 D)
D) 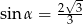
Stosunek boków prostokąta jest równy 1:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 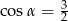 B)
B) 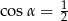 C)
C) 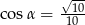 D)
D) 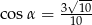
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 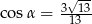 B)
B) 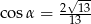 C)
C) 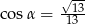 D)
D)