Trójkąt 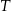 jest podobny do trójkąta
jest podobny do trójkąta 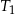 w skali
w skali 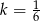 , a trójkąt
, a trójkąt 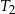 jest podobny do trójkąta
jest podobny do trójkąta 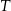 w skali
w skali 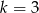 . Pole trójkąta
. Pole trójkąta 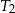 jest równe 24. Trójkąt
jest równe 24. Trójkąt 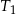 ma pole równe
ma pole równe
A) 12 B) 48 C) 72 D) 96
/Szkoła średnia/Zadania testowe/Geometria
Trójkąt 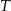 jest podobny do trójkąta
jest podobny do trójkąta 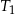 w skali
w skali 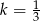 , a trójkąt
, a trójkąt 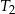 jest podobny do trójkąta
jest podobny do trójkąta 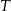 w skali
w skali 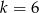 . Pole trójkąta
. Pole trójkąta 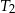 jest równe 32. Trójkąt
jest równe 32. Trójkąt 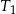 ma pole równe
ma pole równe
A) 128 B) 8 C) 16 D) 24
Kąt wpisany w okrąg o promieniu 6, który jest oparty na łuku długości 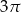 ma miarę
ma miarę
A) 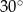 B)
B) 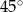 C)
C) 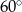 D)
D) 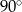
Kąt wpisany w okrąg o promieniu 5, który jest oparty na łuku długości 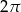 ma miarę
ma miarę
A) 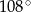 B)
B) 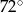 C)
C) 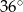 D)
D) 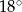
Kąt wpisany w okrąg o promieniu 12, który jest oparty na łuku długości 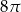 ma miarę
ma miarę
A) 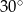 B)
B) 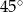 C)
C) 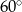 D)
D) 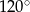
Kąt wpisany w okrąg o średnicy 8, który jest oparty na łuku długości 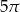 ma miarę
ma miarę
A) 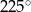 B)
B) 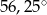 C)
C) 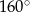 D)
D) 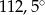
Liczba przekątnych jest równa liczbie boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest o 3 większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest dwa razy większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Dany jest trójkąt prostokątny  o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 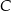 . Jeśli
. Jeśli 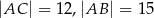 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C)  D)
D) 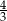
Jedna z przyprostokątnych trójkąta prostokątnego ma długość 15 cm, a przeciwprostokątna 17 cm. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 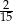 B)
B) 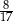 C)
C) 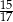 D)
D) 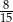
Dany jest trójkąt prostokątny 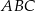 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 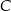 . Jeśli
. Jeśli 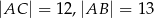 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A) 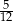 B)
B) 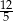 C)
C) 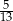 D)
D) 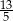
Dany jest trójkąt prostokątny 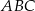 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 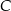 . Jeśli
. Jeśli 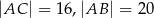 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C) 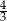 D)
D) 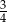
W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8 i jednej z przyprostokątnych 6. Tangens mniejszego kąta ostrego tego trójkąta jest równy
A)  B)
B) 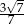 C)
C) 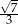 D)
D) 
Promień podstawy walca zwiększamy trzy razy, a jego wysokość zmniejszamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się
Promień podstawy walca zwiększamy cztery razy, a jego wysokość zmniejszamy cztery razy. Wówczas objętość walca
A) nie zmieni się B) zwiększy się o cztery
C) zmniejszy się cztery razy D) zwiększy się cztery razy
Promień podstawy walca zmniejszamy trzy razy, a jego wysokość zwiększamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się
Przekątne podzieliły równoległobok na cztery trójkąty o polach 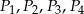 .
.
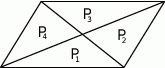
Który z podanych warunków może nie być spełniony?
A) 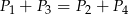 B)
B) 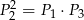 C)
C) 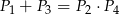 D)
D) 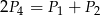
Prostą równoległą do prostej 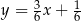 jest prosta:
jest prosta:
A) 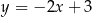 B)
B) 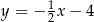 C)
C) 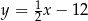 D)
D) 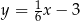
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 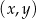 , dana jest prosta
, dana jest prosta 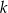 o równaniu
o równaniu 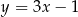 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 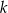 jest prosta o równaniu
jest prosta o równaniu
A) 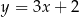 B)
B) 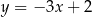 C)
C) 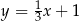 D)
D) 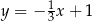
Prostą równoległą do prostej 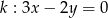 opisuje równanie
opisuje równanie
A) 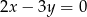 B)
B) 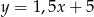 C)
C) 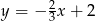 D)
D) 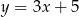
Dana jest prosta 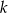 o równaniu
o równaniu 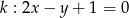 . Spośród podanych prostych wybierz prostą równoległą do
. Spośród podanych prostych wybierz prostą równoległą do 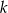 .
.
A) 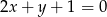 B)
B) 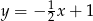 C)
C) 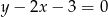 D)
D) 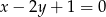
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 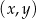 , dana jest prosta
, dana jest prosta 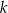 o równaniu
o równaniu 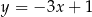 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 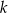 jest prosta o równaniu
jest prosta o równaniu
A) 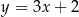 B)
B) 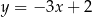 C)
C) 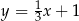 D)
D) 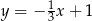
Prostą równoległą do prostej o równaniu 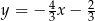 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 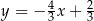 B)
B) 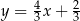 C)
C) 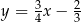 D)
D) 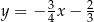
Wskaż równanie prostej równoległej do prostej o równaniu 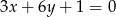 .
.
A) 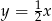 B)
B) 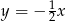 C)
C) 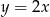 D)
D) 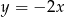
Prosta 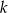 równoległa do prostej
równoległa do prostej 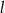 o równaniu
o równaniu 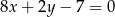 może mieć wzór
może mieć wzór
A) 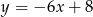 B)
B) 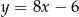 C)
C) 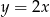 D)
D) 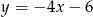
Prostą równoległą do prostej o równaniu 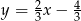 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 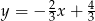 B)
B) 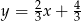 C)
C) 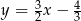 D)
D) 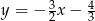
Wskaż równanie prostej równoległej do prostej o równaniu 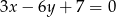 .
.
A) 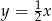 B)
B) 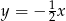 C)
C) 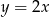 D)
D) 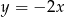
Prosta równoległa do prostej 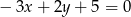 ma równanie:
ma równanie:
A) 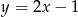 B)
B) 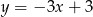 C)
C) 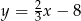 D)
D) 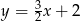
Wskaż równanie prostej równoległej do prostej o równaniu 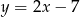 .
.
A) 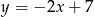 B)
B) 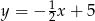 C)
C) 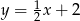 D)
D) 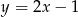
Prosta o równaniu 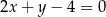 jest równoległa do prostej:
jest równoległa do prostej:
A) 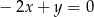 B)
B) 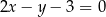 C)
C) 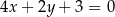 D)
D) 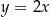
Prosta 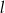 ma równanie
ma równanie 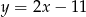 . Wskaż równanie prostej równoległej do
. Wskaż równanie prostej równoległej do 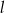 .
.
A) 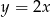 B)
B) 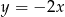 C)
C) 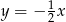 D)
D) 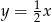
Jeden z kątów ostrych trójkąta prostokątnego ma miarę 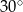 . Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
. Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
A) 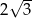 B) 6 C)
B) 6 C) 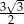 D)
D) 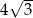
W trójkącie 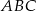 poprowadzono odcinek
poprowadzono odcinek 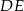 równoległy do boku
równoległy do boku 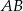 w ten sposób, że
w ten sposób, że 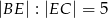 .
.
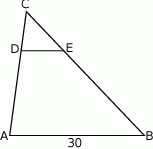
Jeżeli 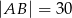 to długość odcinka
to długość odcinka 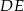 jest równa
jest równa
A) 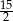 B) 6 C) 5 D)
B) 6 C) 5 D) 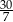
W trójkącie 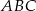 poprowadzono odcinek
poprowadzono odcinek 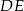 równoległy do boku
równoległy do boku 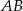 w ten sposób, że
w ten sposób, że 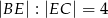 .
.
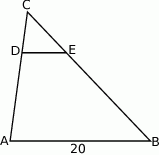
Jeżeli 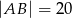 to długość odcinka
to długość odcinka 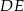 jest równa
jest równa
A) 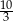 B) 4 C) 5 D)
B) 4 C) 5 D) 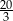
Pole prostokąta 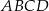 jest równe 90. Na bokach
jest równe 90. Na bokach 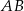 i
i 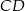 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 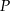 i
i 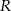 , takie, że
, takie, że 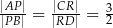 (zobacz rysunek)
(zobacz rysunek)
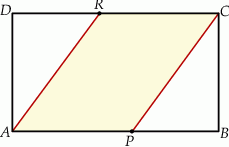
Pole czworokąta 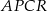 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 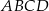 jest równe 90. Na bokach
jest równe 90. Na bokach 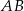 i
i 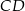 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 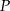 i
i 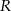 , takie, że
, takie, że 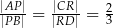 (zobacz rysunek)
(zobacz rysunek)
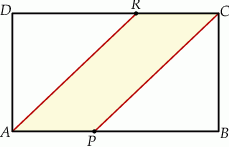
Pole czworokąta 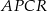 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Z punktu 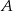 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 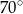 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 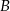 i
i 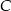 . Punkt
. Punkt 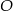 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 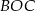 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 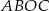 , jest równa
, jest równa
A) 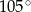 B)
B) 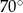 C)
C) 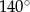 D)
D) 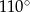
Z punktu 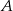 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 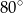 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 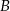 i
i 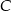 . Punkt
. Punkt 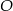 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 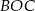 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 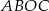 , jest równa
, jest równa
A) 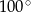 B)
B) 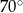 C)
C) 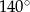 D)
D) 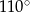
Z punktu 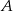 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 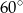 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 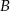 i
i 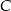 . Punkt
. Punkt 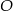 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 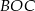 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 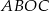 , jest równa
, jest równa
A) 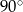 B)
B) 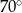 C)
C) 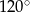 D)
D) 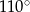
Końcami odcinka 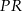 są punkty
są punkty 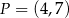 i
i 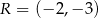 . Odległość punktu
. Odległość punktu 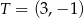 od środka odcinka
od środka odcinka 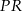 jest równa
jest równa
A) 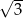 B)
B) 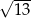 C)
C) 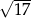 D)
D) 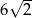
Końcami odcinka 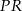 są punkty
są punkty 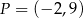 i
i 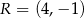 . Odległość punktu
. Odległość punktu 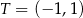 od środka odcinka
od środka odcinka 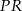 jest równa
jest równa
A) 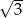 B)
B) 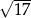 C)
C) 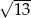 D)
D) 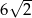
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna tego trójkąta ma długość
A) 24 B) 20 C) 14 D) 18
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 4. Wysokość ta dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna jest równa
A) 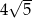 B)
B) 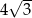 C) 10 D) 8
C) 10 D) 8
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 8 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 20 B) 16 C) 8 D) 18
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 12. Przeciwprostokątna tego trójkąta ma długość
A) 15 B) 24 C) 16 D) 3
W trójkącie równoramiennym 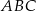 o podstawie
o podstawie 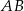 dane są:
dane są: 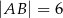 oraz
oraz 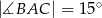 . Pole koła opisanego na tym trójkącie jest równe
. Pole koła opisanego na tym trójkącie jest równe
A) 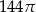 B)
B) 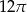 C)
C) 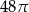 D)
D) 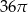
W trójkącie równoramiennym o bokach długości: 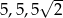 kąt przy podstawie ma miarę:
kąt przy podstawie ma miarę:
A) 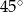 B)
B) 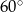 C)
C) 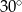 D)
D) 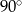
Podstawą ostrosłupa jest kwadrat 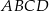 o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 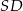 , a długość krawędzi
, a długość krawędzi 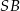 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
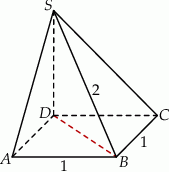
Różnica miar kątów 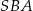 i
i 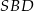 jest równa
jest równa
A) 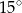 B)
B) 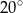 C)
C) 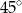 D)
D) 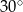
Objętość walca wynosi 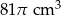 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 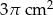 B)
B) 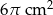 C)
C) 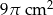 D)
D) 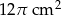
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
A) 512 B) 384 C) 96 D) 16
Pole koła opisanego na trójkącie równobocznym o wysokości 9 jest równe
A) 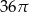 B)
B) 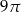 C)
C) 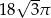 D)
D) 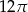
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
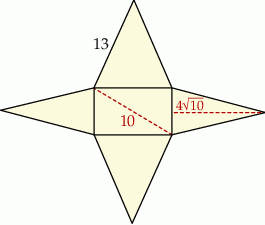
Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384

