Agata ozdabia kartkę, czyli jak nie układać zadań egzaminacyjnych

Egzamin ósmoklasisty

Pierwsze zadanie, które wywołało niedawno sporo kontrowersji, to zadanie z próbnego egzaminu ósmoklasisty.

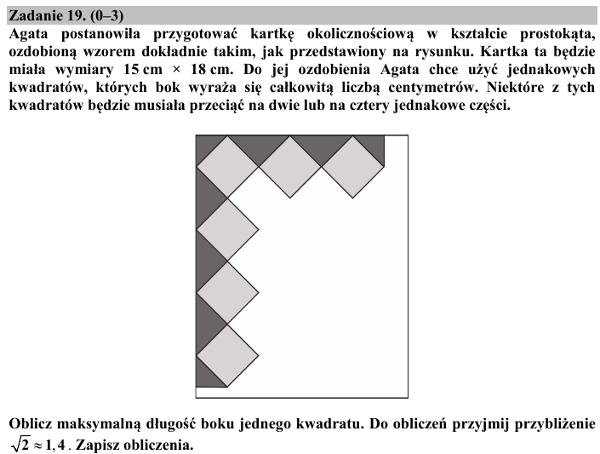
Każdy kto próbował rozwiązać to zadanie z pewnością zmierzył się wątpliwościami, o co w zasadzie tej Agacie chodzi? Co gorsza, aspekt praktyczny tego zadania jest absurdalny (np. absurdalne założenie o całkowitej długości boku), więc jesteśmy zmuszeni ustalić, jakimi ścieżkami podążał pokrętny umysł autora tego zadania, a nie biednej Agaty.

Ale konkretniej, w poleceniu zadania jesteśmy pytani o maksymalną długość boku kwadratu, którego można użyć do przygotowania wzoru, co jest sprzeczne z informacją o tym, że wzór jest "dokładnie taki jak na rysunku". Najwyraźniej jednak nie dokładnie taki sam, skoro możemy zmieniać długość boku kwadratu. I tu zaczyna się problem – co jeszcze możemy zmieniać? Liczbę kwadratów? – jeżeli tak, to jak łatwo sprawdzić odpowiedzią do zadania będzie kwadrat o boku 10 cm. Zresztą nie jest jasne (nie jest sprecyzowane w treści), czy rysunek przedstawia tylko fragment wzoru, czy całą kartkę ze wzorem. Poza tym nie wiadomo, czy kwadraty mają wypełnić całą kartkę, czy tylko ten boczny pasek. W treści zadania jest też informacja, o tym że niektóre kwadraty będzie musiała pociąć na dwie lub cztery części – tymczasem na rysunku jest 5 połówek i trzy ćwiartki ; co się stało z pozostałymi częściami pociętych kwadratów? I tak dalej, i tak dalej.

Wszystko to może brzmieć jak czysto akademickie rozważania, ale tak nie jest – rozmawialiśmy z wieloma uczniami, którzy z dużym wysiłkiem próbowali zrozumieć o co chodzi w tym zadaniu. Co gorsza, najczęściej dotyczyło to uczniów dobrych i bardzo dobrych, którzy nie czytają treści bezmyślnie. Sam też miałem duży problem z ustaleniem, o co może chodzić autorowi tego zadania. Podsunąłem też to zadanie kilku zawodowym matematykom i wszyscy bez wyjątku wskazywali na brak precyzji w treści, uniemożliwiający jednoznaczne rozwiązanie tego zadania. Dostaliśmy też już kilkanaście listów od nauczycieli wskazujących na problemy jakie sprawiła uczniom ta nieszczęsna kartka okolicznościowa.

Na osobną uwagę zasługuje też zupełnie sztuczny i bezsensowny "kontekst praktyczny". Były już takie czasy, gdy mieliśmy nawet całe arkusze zadań tematycznych osadzonych w absurdalnym kontekście praktycznym. Niestety, przy braku treści matematycznych, które mogłyby być sprawdzane na teście ósmoklasisty, takich kwiatków będzie pewnie coraz więcej.

Pozostając w zakresie testu ósmoklasisty, warto zwrócić uwagę na ostatnie zadanie tegorocznego testu egzaminacyjnego.

Pytanie brzmi: w jaki sposób obliczyć długość odcinka TS? Sprawa jest banalnie prosta, jeżeli mamy podobieństwo trójkątów lub twierdzenie Talesa. Tymczasem włożono bardzo dużo wysiłku w usunięcie podobieństwa z wymagań egzaminacyjnych. W rezultacie, w treści zadania faktycznie zamieszczono tezę twierdzenia Talesa - informację o tym, że odcinek łączący środki boków trójkąta jest równoległy do jego boku - to pozwala obliczyć długość tego odcinka np. z twierdzenia Pitagorasa. Efekt końcowy był jednak taki, że dla uczniów, którzy nie znali podobieństwa trójkątów lub twierdzenia Talesa treść zadania była dużo bardziej podchwytliwa i samo zadanie trudniejsze. Bardzo chciałbym zobaczyć jak autor tego zadania uzasadnia równoległość odcinków TS i PR bez użycia twierdzenia Talesa i podobieństwa trójkątów.

Morał z tego taki, że wymagania egzaminacyjne należy traktować z przymrużeniem oka i jeżeli tylko mamy czas, siłę i wystarczająco dobrych uczniów, to warto wykraczać poza te ramy.

Egzamin gimnazjalny

Kolejne niezwykle "praktyczne" zadanie – tym razem z egzaminu gimnazjalnego.

Widziałem na żywo jak uczniowie męczą się z tym zadaniem. Problemów jest kilka. Po pierwsze, w treści zadania 11 mamy po raz kolejny magiczne sformułowanie "w jeden z trzech sposobów przedstawionych na powyższych rysunkach". Brzmi niewinnie, ale co w zasadzie jest przedstawione na tych rysunkach? Na przykład na pierwszym z nich jest trójkąt złożony z trzech stolików. Tymczasem, mamy ustawić w ten sposób 36 stolików. To oznacza, że jednak musimy to zrobić jakoś inaczej, bo na rysunku są trzy stoliki. No i musimy się domyślić, że autorowi chodzi o 12 takich trójkątów po trzy stoliki. Dla uczniów jednak wcale nie było to takie oczywiste i widziałem bardzo dobrych uczniów, którzy próbowali ustawić te stoliki w jeden duży trójkąt, albo jeden duży sześciokąt. I trudno im się dziwić, bo treść zadania jest w tym zakresie bardzo nieprecyzyjna.

Jeszcze większy problem jest z zadaniem 12. Możemy się domyślać, że w intencji autora na oba pytania należy udzielić odpowiedzi twierdzącej. Jeżeli jednak spróbujemy znaleźć precyzyjne argumenty dla prawdziwości tych zdań, to sprawa jest bardziej skomplikowana, niż może się wydawać. Np. w przypadku drugiego pytania najprościej jest dodatkowo założyć, że figura na drugim rysunku to sześciokąt foremny – prawdopodobnie tak właśnie postąpiła znakomita większość uczniów. Jednak lepsi uczniowie mieli z tym problem, bo takiej informacji nie ma w treści zadania. I te uzasadnione wątpliwości sprawiały, że zadanie stawało się znacznie trudniejsze.

Mamy więc kolejny przykład zadania, które premiuje uczniów słabych, którzy nie mają problemu z samodzielnym dodawaniem założeń ułatwiających im dojście do z góry założonej tezy. Niezbyt mi się to podoba.

Jeszcze jedna perełka z egzaminu gimnazjalnego.

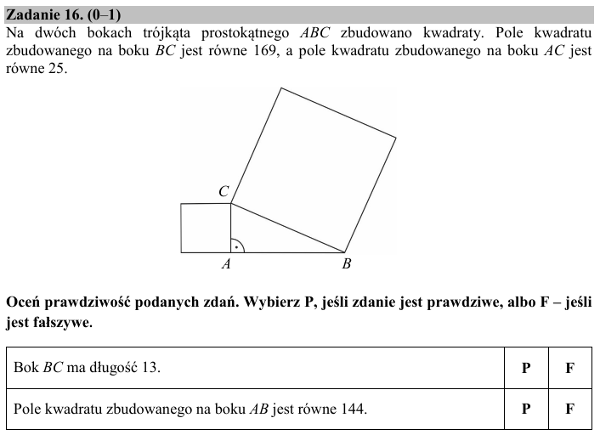
Dla każdego nauczyciela matematyki intencje autora są oczywiste – proste zadanie na twierdzenie Pitagorasa. Sam też uznałbym to za proste i standardowe zadanie, gdybym nie widział uczniów zaznaczających natychmiast fałsz w drugim pytaniu. I trudno odmówić racji ich argumentacji: z treści zadania jednoznacznie wynika, że kwadraty zbudowano na dwóch bokach trójkąta: BC i AC. Z treści jednoznacznie wynika, że na boku AB nie zbudowano żadnego kwadratu. Dlatego drugie zdanie jest fałszywe. Szczerze mówiąc, nie podjąłbym się dyskusji z tą argumentacją – moim zdaniem odpowiedź "fałsz" jest dobrą odpowiedzią w drugim pytaniu. A wszystko przez brak wyobraźni autora zadania – wystarczyło przecież inaczej sformułować drugie pytanie.

Matura

Na deser ostanie zadanie z matury rozszerzonej (stara formuła).

Żeby zrozumieć jakie problemy wiążą się z tym zadaniem, najlepiej jest spróbować samemu je rozwiązać. Jak wyjaśniliśmy w naszym rozwiązaniu, podane w treści zadania informacje o przystawaniu przeciwległych ścian bocznych są zupełnie niepotrzebne i trudno zrozumieć po co zostały podane. W szczególności, nie ułatwiają one rozwiązania zadania, a wręcz przeciwnie – jeżeli spróbujemy je wykorzystać, to stajemy przed dylematem, które krawędzie tych trójkątów są sobie równe (to wcale nie jest oczywiste).

Kolejny problem, to pytanie, czy w odpowiedzi możemy użyć zdefiniowanych w treści zadania kątów \(\alpha\) i \(\beta\)? Dla przykładu proszę zajrzeć do treści i odpowiedzi do jednego z zadań matury rozszerzonej z czerwca 2017 (stara formuła). W przytoczonym powyżej zadaniu z tegorocznej matury bardzo łatwo jest otrzymać odpowiedź w postaci \(576+\frac{288}{\cos\alpha}+\frac{288}{\cos \beta}\). Okazuje się jednak, że odpowiedź tę można uprościć do konkretnej liczby 1416. Pytanie brzmi: jak będą punktowane te odpowiedzi? Można się domyślać, że maksymalną liczbę punktów będzie można otrzymać tylko za drugą odpowiedź, co moim zdaniem będzie błędem i będzie bardzo krzywdzące dla uczniów.

Taki podobny przykład jaki mi przychodzi do głowy w tym kontekście, to zadanie w stylu

I teraz wyobraźmy sobie, że maksymalną liczbę punktów można otrzymać tylko za odpowiedź 9, a nie np. za \(3a\), \(3b\) czy \(a+b+3\). Kompletnie bez sensu.

Pomóżmy Agacie

Uważni użytkownicy naszego serwisu zapewne zauważali, że staramy się zawsze poprawiać treści zadań, tak żeby usunąć ewentualne niejednoznaczności. Tak też się stało w przypadku opisanych wyżej zadań, z jednym wyjątkiem. Wciąż nie wiemy jak pomóc Agacie z jej kartką – w treści tego zadania jest tyle problemów, że najprościej byłoby po prostu ułożyć je zupełnie od nowa. Na dzień dzisiejszy zadanie to funkcjonuje z oryginalną treścią i w efekcie stale generuje nowe komentarze z prośbą o poprawienie jego treści. Może ma ktoś dobry pomysł jak przywrócić sens temu zadaniu?