Na środkowej 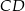 trójkąta
trójkąta 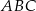 wybrano punkt
wybrano punkt 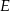 . Wykaż, że trójkąty
. Wykaż, że trójkąty 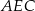 i
i 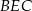 mają równe pola.
mają równe pola.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
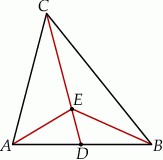
Na środkowej 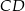 trójkąta
trójkąta 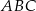 wybrano punkt
wybrano punkt 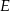 . Wykaż, że trójkąty
. Wykaż, że trójkąty 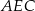 i
i 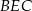 mają równe pola.
mają równe pola.

Punkt 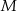 przyprostokątnej
przyprostokątnej 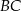 trójkąta prostokątnego
trójkąta prostokątnego 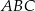 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 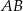 otrzymując punkt
otrzymując punkt 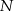 . Wykaż, że
. Wykaż, że 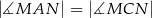 .
.
Dany jest trójkąt ostrokątny równoramienny 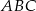 , w którym bok
, w którym bok 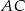 jest równy
jest równy 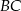 . Odcinek
. Odcinek 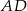 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 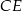 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 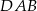 jest równy kątowi
jest równy kątowi 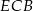 .
.
Oblicz długości odcinka 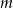 .
.
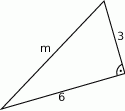
Oblicz długości odcinka 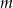 .
.
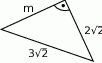
Oblicz długości odcinka 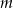 .
.
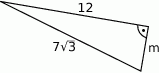
Oblicz miarę kąta  .
.
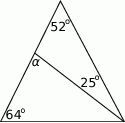
Oblicz miarę kąta  .
.
Oblicz miarę kąta  .
.
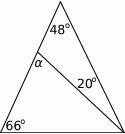
Oblicz miarę kąta  .
.
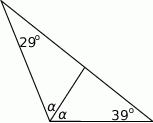
Oblicz miarę kąta  .
.
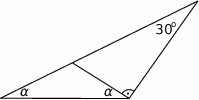
Oblicz miarę kąta  .
.
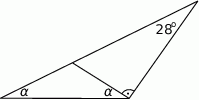
Oblicz miarę kąta  .
.
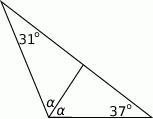
Oblicz miarę kąta  .
.
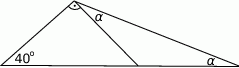
Oblicz miarę kąta  .
.
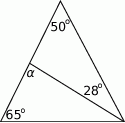
Liczby 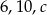 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Prosta 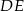 jest równoległa do boku
jest równoległa do boku 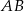 trójkąta
trójkąta 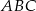 i przecina bok
i przecina bok 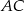 w punkcie
w punkcie 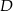 , bok
, bok 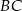 w punkcie
w punkcie 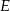 . Oblicz
. Oblicz 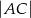 jeśli
jeśli 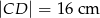 ,
, 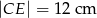 i
i 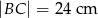 .
.
Prosta 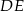 jest równoległa do boku
jest równoległa do boku 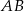 trójkąta
trójkąta 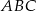 i przecina bok
i przecina bok 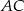 w punkcie
w punkcie 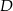 , bok
, bok 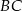 w punkcie
w punkcie 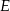 . Oblicz
. Oblicz 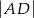 jeśli
jeśli 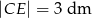 ,
, 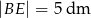 i
i 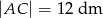 .
.
Prosta 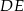 jest równoległa do boku
jest równoległa do boku 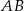 trójkąta
trójkąta 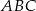 i przecina bok
i przecina bok 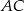 w punkcie
w punkcie 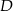 , bok
, bok 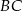 w punkcie
w punkcie 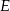 . Oblicz
. Oblicz 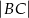 , jeśli
, jeśli 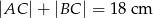 ,
, 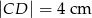 i
i 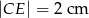 .
.
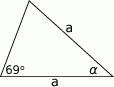
Oblicz pole trójkąta przedstawionego na rysunku.
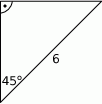
Oblicz pole trójkąta przedstawionego na rysunku.
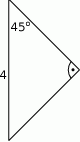
Jaka jest miara kąta  ?
?
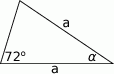
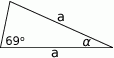
Jaka jest miara kąta  ?
?
Jaka jest miara kąta  ?
?
Wierzchołek 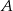 trójkąta ostrokątnego
trójkąta ostrokątnego 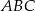 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 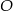 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 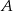 poprowadzono wysokość
poprowadzono wysokość 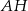 . Wykaż, że
. Wykaż, że 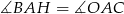 .
.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
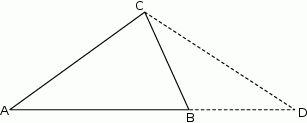
W trójkącie 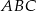 przedłużono bok
przedłużono bok 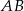 poza wierzchołek
poza wierzchołek 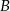 i odłożono odcinek
i odłożono odcinek 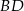 taki, że
taki, że 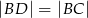 . Następnie połączono punkty
. Następnie połączono punkty 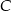 i
i 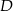 (rysunek). Wykaż, że
(rysunek). Wykaż, że 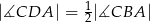 .
.
W trójkącie 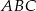 przedłużono bok
przedłużono bok 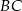 poza wierzchołek
poza wierzchołek 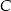 i odłożono odcinek
i odłożono odcinek 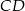 taki, że
taki, że 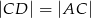 . Następnie połączono punkty
. Następnie połączono punkty 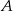 i
i 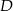 (rysunek). Wykaż, że
(rysunek). Wykaż, że 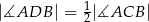 .
.
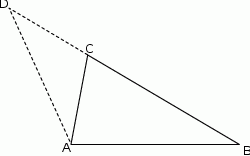
Na dwusiecznej 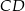 trójkąta
trójkąta 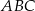 , w którym
, w którym 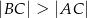 wybrano punkt
wybrano punkt 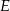 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 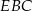 jest większe od pola trójkąta
jest większe od pola trójkąta 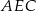 .
.
Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku tego trójkąta.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 2 cm krótsza od boku tego trójkąta.
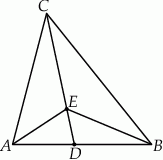
W trójkącie 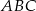 dane są:
dane są: 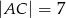 ,
, 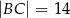 i
i 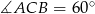 . Oblicz pole trójkąta
. Oblicz pole trójkąta 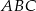 .
.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Jaką wysokość ma trójkąt równoboczny o boku 4?
Oblicz pole trójkąta przedstawionego na rysunku.
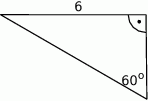
Oblicz pole trójkąta przedstawionego na rysunku.
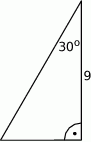
Dwusieczne kątów przyległych do boku 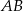 trójkąta
trójkąta 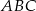 przecinają się w punkcie
przecinają się w punkcie 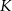 . Odległość punktu
. Odległość punktu 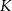 od odcinka
od odcinka 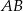 wynosi 3. Jaka jest odległość punktu
wynosi 3. Jaka jest odległość punktu 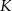 od odcinka
od odcinka 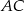 ?
?
