W trójkącie 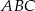 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta  i przez punkt
i przez punkt  przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem  prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 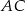 i
i 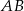 , które przecinają te boki odpowiednio w punktach
, które przecinają te boki odpowiednio w punktach 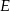 i
i 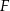 . Wykaż, że czworokąt
. Wykaż, że czworokąt 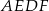 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
/Szkoła podstawowa/Geometria/Trójkąt
Dany jest trójkąt równoramienny o bokach długości 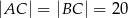 i
i 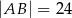 . Odcinek
. Odcinek 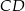 jest wysokością trójkąta
jest wysokością trójkąta  , a odcinek
, a odcinek  jest wysokością trójkąta
jest wysokością trójkąta  (zobacz rysunek).
(zobacz rysunek).
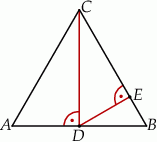
Oblicz długość odcinka 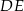 .
.
Dwa spośród boków trójkąta równoramiennego mają długości 3 cm i 4 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 5 cm i 9 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 5 cm i 11 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 2 cm i 5 cm. Jaką długość może mieć trzeci bok?
Na rysunku przedstawiono trójkąt 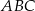 , w którym
, w którym 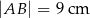 oraz odcinek
oraz odcinek 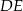 równoległy do boku
równoległy do boku 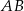 trójkąta, którego długość jest równa 6 cm.
trójkąta, którego długość jest równa 6 cm.
Pole trójkąta  jest równe
jest równe  , a pole trapezu
, a pole trapezu 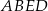 jest o 25% większe od pola trójkąta
jest o 25% większe od pola trójkąta 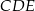 . Oblicz wysokość trapezu
. Oblicz wysokość trapezu 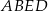 .
.
Liczby 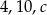 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 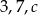 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 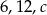 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 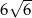 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
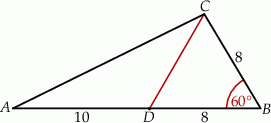
Oblicz pole trójkąta, którego wymiary podano na rysunku.
Punkt 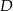 jest środkiem boku
jest środkiem boku 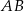 trójkąta
trójkąta 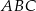 , w którym
, w którym 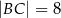 ,
, 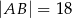 i
i 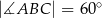 . Oblicz pole trójkąta
. Oblicz pole trójkąta 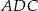 .
.
W trójkącie 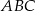 , w którym
, w którym 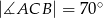 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 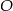 z wierzchołkami
z wierzchołkami 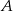 i
i 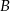 . Oblicz miarę kąta
. Oblicz miarę kąta 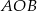 .
.
Oblicz pole trójkąta równoramiennego, w którym odległość wierzchołka kąta prostego od przeciwprostokątnej jest równa 5 cm.
Punkty  są środkami boków trójkąta
są środkami boków trójkąta  . Pole trójkąta
. Pole trójkąta 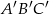 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 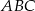 .
.
Uzasadnij, że oba kąty przy podstawie 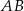 trójkąta
trójkąta 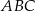 są równe.
są równe.
Środkowa  trójkąta
trójkąta 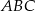 ma długość równą połowie długości boku
ma długość równą połowie długości boku 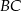 . Miara kąta między tą środkową a wysokością
. Miara kąta między tą środkową a wysokością 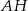 jest równa
jest równa 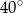 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 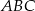 .
.
Jaka jest długość boku trójkąta równobocznego o polu 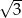 ?
?
Trójkąty 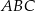 i
i 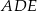 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 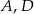 i
i 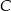 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 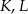 i
i 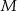 są środkami odcinków
są środkami odcinków 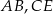 i
i  . Wykaż, że
. Wykaż, że 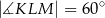 .
.
Kąt przy podstawie trójkąta równoramiennego 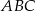 ma miarę
ma miarę 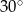 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta  .
.
Z wierzchołka kąta prostego trójkąta prostokątnego 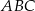 poprowadzono wysokość
poprowadzono wysokość 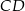 , która podzieliła przeciwprostokątną
, która podzieliła przeciwprostokątną 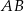 na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
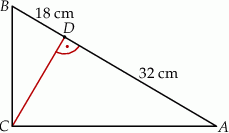
Oblicz pole trójkąta  .
.
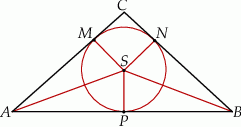
W trójkąt równoramienny 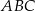 (
(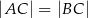 ) wpisano okrąg o środku
) wpisano okrąg o środku 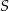 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 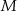 ,
, 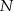 i
i 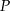 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 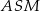 i
i 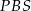 są przystające.
są przystające.
Dwa spośród boków trójkąta mają długości 3 i 5. Zaznacz na osi liczbowej wszystkie liczby oznaczające możliwe długości trzeciego boku.
Dany jest trójkąt  . Punkt
. Punkt  jest środkiem boku
jest środkiem boku  tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 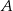 i
i 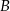 od prostej
od prostej 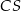 są równe.
są równe.
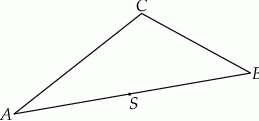
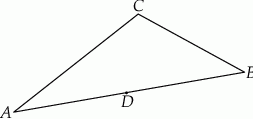
Na boku 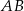 trójkąta
trójkąta 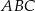 wybrano punkt
wybrano punkt  w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 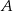 i
i 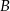 od prostej
od prostej 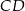 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 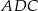 i
i 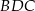 mają równe pola.
mają równe pola.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.

