Długości podstaw trapezu równoramiennego są równe  oraz
oraz 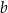 , przy czym
, przy czym 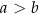 . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od
. W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od 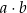 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny opisany na okręgu/Udowodnij...
Pole trapezu równoramiennego opisanego na okręgu jest równe 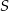 , a kąt ostry przy podstawie ma miarę
, a kąt ostry przy podstawie ma miarę  . Wykaż, że ramię tego trapezu ma długość
. Wykaż, że ramię tego trapezu ma długość 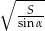 .
.
Na okręgu o promieniu  opisano trapez równoramienny, którego kąt ostry ma miarę
opisano trapez równoramienny, którego kąt ostry ma miarę  . Wykaż, że promień okręgu opisanego na tym czworokącie jest równy
. Wykaż, że promień okręgu opisanego na tym czworokącie jest równy 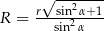 .
.
Dany jest trapez równoramienny 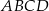 o obwodzie
o obwodzie 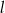 i podstawach
i podstawach 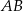 oraz
oraz 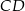 takich, że
takich, że 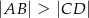 . Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna
. Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna 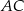 trapezu ma długość
trapezu ma długość 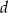 (zobacz rysunek).
(zobacz rysunek).
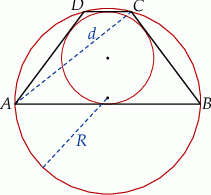
Wykaż, że promień 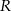 okręgu opisanego na trapezie
okręgu opisanego na trapezie 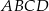 jest równy
jest równy 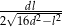 .
.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Ukryj
Podobne zadania
Trapez równoramienny 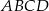 o podstawach
o podstawach 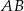 i
i 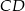 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 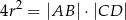 .
.

