Dłuższa przekątna równoległoboku o kącie ostrym 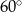 ma długość
ma długość 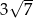 . Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
. Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Różne
Kąt ostry równoległoboku ma miarę 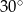 . Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
. Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
Punkty 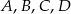 są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku
są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku 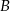 ma miarę
ma miarę 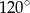 i promień okręgu wpisanego w trójkąt
i promień okręgu wpisanego w trójkąt 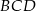 jest równy
jest równy 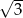 , oblicz długości boków i pole tego równoległoboku.
, oblicz długości boków i pole tego równoległoboku.
Kąt ostry równoległoboku ma miarę 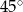 . Punkt wspólny przekątnych równoległoboku jest oddalony od boków o
. Punkt wspólny przekątnych równoległoboku jest oddalony od boków o 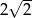 i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
W równoległoboku 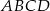 , w którym
, w którym 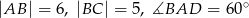 poprowadzono wysokości
poprowadzono wysokości 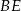 i
i 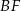 na boki
na boki 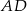 i
i 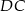 .
.
- Wykonaj odpowiedni rysunek i oblicz długości odcinków
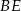 i
i 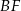 .
. - Oblicz pole trójkąta
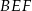 .
.

