Zależność między temperaturą wyrażoną w stopniach Fahrenheita, a wyrażoną w stopniach Celsjusza jest zależnością liniową.
- Znajdź tę zależność wiedząc ze
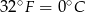 , a
, a 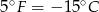 .
. - 22 lipca w San Diego temperatura o godzinie
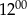 była o
była o 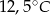 wyższa niż temperatura o godzinie
wyższa niż temperatura o godzinie 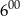 . Wyraź wzrost temperatury w stopniach Fahrenheita.
. Wyraź wzrost temperatury w stopniach Fahrenheita.

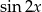 i
i 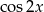 jeśli wiadomo że
jeśli wiadomo że 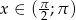 i
i 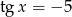 .
. 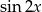 i
i 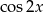 jeśli wiadomo, że
jeśli wiadomo, że 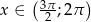 i
i 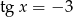 .
. 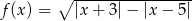 .
. 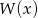 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 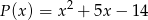 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 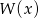 przez dwumian
przez dwumian 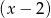 otrzymujemy resztę 18.
otrzymujemy resztę 18. 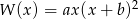 i
i 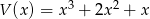 są równe. Oblicz
są równe. Oblicz  i
i 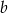 .
. 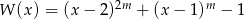 jest podzielny przez wielomian
jest podzielny przez wielomian 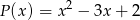 dla każdego
dla każdego 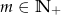 .
. 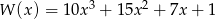 .
. 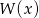 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. 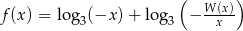 .
.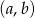 , dla których funkcja
, dla których funkcja 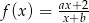 jest funkcją homograficzną, malejącą w każdym z przedziałów:
jest funkcją homograficzną, malejącą w każdym z przedziałów: 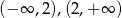 .
. 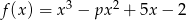 .
. 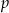 , dla której funkcja
, dla której funkcja 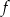 osiąga minimum w punkcie
osiąga minimum w punkcie 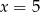 .
. 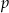 podaj przedziały monotoniczności funkcji
podaj przedziały monotoniczności funkcji 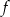 .
.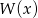 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 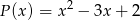 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 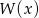 przez dwumian
przez dwumian 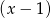 otrzymujemy resztę 5.
otrzymujemy resztę 5. 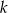 , dla których funkcja
, dla których funkcja 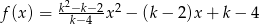 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe. 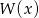 przez dwumian
przez dwumian 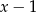 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 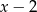 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 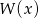 przez wielomian
przez wielomian 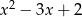 .
. 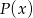 przez trójmian
przez trójmian 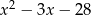 jeśli
jeśli 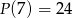 i
i 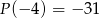 .
.  , taki, że
, taki, że 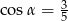 i
i 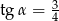 .
. 