Wyznacz najmniejszą i największą wartość funkcji 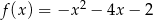 w przedziale
w przedziale 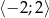 .
.
/Szkoła średnia/Funkcje
Wyznacz największą i najmniejszą wartość funkcji 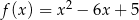 osiąganą w przedziale
osiąganą w przedziale 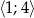 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 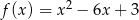 w przedziale
w przedziale 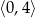 .
.
Oblicz najmniejszą i największą wartość funkcji 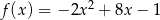 w przedziale
w przedziale 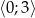 .
.
Wyznacz wartość największą i najmniejszą funkcji kwadratowej 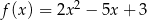 w przedziale
w przedziale 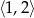 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 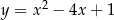 w przedziale
w przedziale 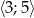 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 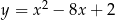 w przedziale
w przedziale 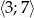 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 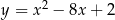 w przedziale
w przedziale 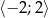 .
.
Wyznacz najmniejszą i największą wartość funkcji 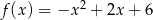 w przedziale
w przedziale 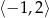 .
.
Oblicz najmniejszą i największą wartość funkcji 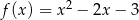 w przedziale
w przedziale 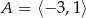 .
.
Oblicz najmniejszą i największą wartość funkcji 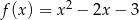 w przedziale
w przedziale 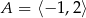 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 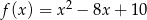 w przedziale
w przedziale 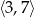 .
.
Wyznacz największą i najmniejszą wartość funkcji 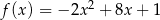 osiąganą w przedziale
osiąganą w przedziale 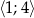 .
.
Wyznacz największą i najmniejszą wartość funkcji 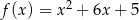 osiąganą w przedziale
osiąganą w przedziale 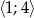 .
.
Oblicz największą i najmniejszą wartość funkcji 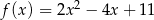 w przedziale
w przedziale 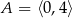 .
.
Oblicz najmniejszą i największą wartość funkcji 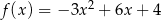 w przedziale
w przedziale 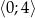 .
.
Suma reszt jakie otrzymujemy dzieląc wielomian 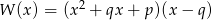 przez dwumiany
przez dwumiany 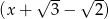 i
i 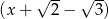 jest równa
jest równa 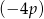 , gdzie
, gdzie 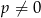 . Oblicz
. Oblicz 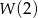 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 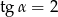 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 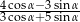 .
.
Kąt  jest ostry i
jest ostry i 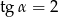 . Oblicz
. Oblicz 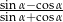 .
.
Oblicz wartość wyrażenia 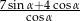 jeżeli
jeżeli  jest takim kątem ostrym, że
jest takim kątem ostrym, że 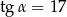 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 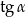 =3, oblicz wartość wyrażenia
=3, oblicz wartość wyrażenia 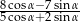 .
.
Oblicz wartość wyrażenia 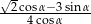 wiedząc, że
wiedząc, że 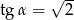 i
i 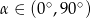 .
.
Dana jest funkcja liniowa 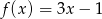 .
.
- Rozwiąż nierówność
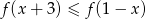 .
. - Podaj maksymalne przedziały monotoniczności funkcji
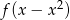 .
.
Wielomian 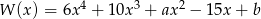 jest podzielny przez trójmian
jest podzielny przez trójmian 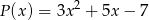 . Wyznacz liczby
. Wyznacz liczby  i
i 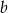 .
.
Wyznacz miejsca zerowe funkcji
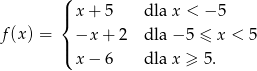
Wykaż, że dla dowolnego kąta  prawdziwa jest tożsamość
prawdziwa jest tożsamość 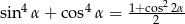 .
.
- Sprawdź, czy równość
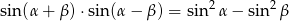
jest tożsamością trygonometryczną.
- Udowodnij, że jeżeli
 i
i 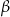 są dwoma kątami trójkąta i
są dwoma kątami trójkąta i 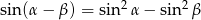 , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
, to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Funkcje 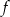 i
i 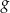 są określone wzorami:
są określone wzorami: 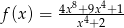 i
i 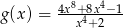 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wykaż, że
. Wykaż, że 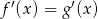 .
.
Wyznacz dziedzinę funkcji 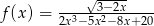 .
.
Dla jakich wartości parametru 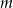 funkcja
funkcja 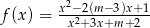 jest określona dla każdego
jest określona dla każdego 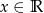 i ma dwa różne miejsca zerowe?
i ma dwa różne miejsca zerowe?
Wyznacz dziedzinę funkcji 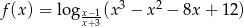 .
.
Wyznacz dziedzinę funkcji 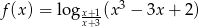 .
.
Określ zbiór wartości funkcji: 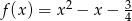 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Dana jest funkcja kwadratowa 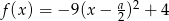
- Dla
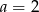 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. - Dla
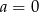 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne. - Wyznacz
 tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 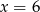 .
.
Oblicz wartość wyrażenia 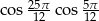 .
.
Wyznacz zbiór wartości funkcji 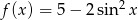 dla
dla 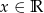 .
.
Wyznacz zbiór wartości funkcji 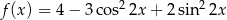 dla
dla 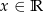 .
.
Podaj wartość wyrażenia 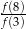 jeżeli
jeżeli 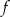 jest funkcją kwadratową o miejscach zerowych 2 i 4.
jest funkcją kwadratową o miejscach zerowych 2 i 4.
Liczby 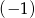 i 3 są miejscami zerowymi funkcji kwadratowej
i 3 są miejscami zerowymi funkcji kwadratowej 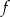 . Oblicz
. Oblicz 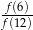 .
.
Miejscami zerowymi funkcji kwadratowej 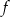 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 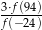 .
.
Wiedząc, że zbiorem wartości funkcji 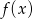 jest przedział
jest przedział 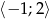 wyznacz wszystkie wartości
wyznacz wszystkie wartości 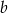 , dla których funkcja
, dla których funkcja 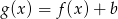 nie ma miejsc zerowych.
nie ma miejsc zerowych.
Dany jest wielomian 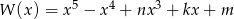 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 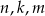 dla których reszta z dzielenia wielomianu
dla których reszta z dzielenia wielomianu 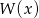 przez wielomian
przez wielomian 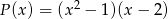 jest równa
jest równa 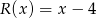 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 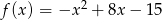 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 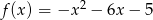 .
.

