Znajdź najmniejszą i największą wartość funkcji 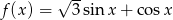 w przedziale
w przedziale 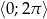 .
.
/Szkoła średnia/Funkcje
Znajdź najmniejszą i największą wartość funkcji 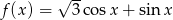 w przedziale
w przedziale 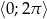 .
.
Wykaż, że jeżeli 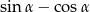 jest liczbą wymierną to wymierna jest również liczba
jest liczbą wymierną to wymierna jest również liczba 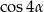 .
.
Dla jakich wartości parametru 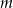 dziedziną funkcji
dziedziną funkcji 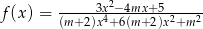 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Oblicz wartość wyrażenia 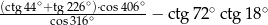 .
.
Wyznacz resztę z dzielenia wielomianu 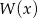 przez wielomian
przez wielomian 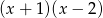 wiedząc, że
wiedząc, że 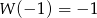 i
i 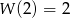 .
.
Wyznacz resztę z dzielenia wielomianu 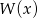 przez wielomian
przez wielomian 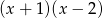 wiedząc, że
wiedząc, że 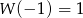 i
i 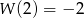 .
.
Wyznacz resztę z dzielenia wielomianu 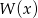 przez wielomian
przez wielomian 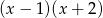 wiedząc, że
wiedząc, że 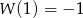 i
i 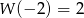 .
.
Funkcja 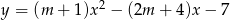 jest malejąca w zbiorze
jest malejąca w zbiorze 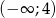 i rosnąca w zbiorze
i rosnąca w zbiorze 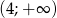 . Wyznacz parametr
. Wyznacz parametr 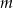 .
.
Dana jest funkcja 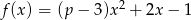 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 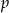 , dla których:
, dla których:
- największa wartość funkcji
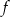 jest liczbą ujemną,
jest liczbą ujemną, - najmniejsza wartość funkcji
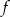 jest mniejsza od -2.
jest mniejsza od -2.
Wielomian 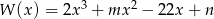 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 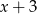 i
i 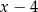 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 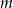 oraz rozwiąż nierówność
oraz rozwiąż nierówność 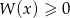 .
.
Wielomian określony wzorem 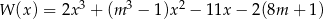 jest podzielny przez dwumian
jest podzielny przez dwumian 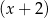 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 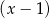 daje resztę 12. Oblicz
daje resztę 12. Oblicz 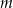 i dla wyznaczonej wartości
i dla wyznaczonej wartości 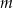 rozwiąż nierówność
rozwiąż nierówność 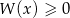 .
.
Wielomian określony wzorem 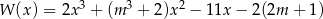 jest podzielny przez dwumian
jest podzielny przez dwumian 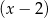 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 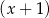 daje resztę 6. Oblicz
daje resztę 6. Oblicz 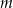 oraz pierwiastki wielomianu
oraz pierwiastki wielomianu 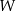 dla wyznaczonej wartości
dla wyznaczonej wartości 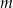 .
.
Wielomian określony wzorem 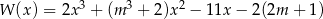 jest podzielny przez dwumian
jest podzielny przez dwumian 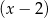 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 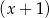 daje resztę 6. Oblicz
daje resztę 6. Oblicz 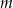 i dla wyznaczonej wartości
i dla wyznaczonej wartości 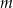 rozwiąż nierówność
rozwiąż nierówność 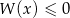 .
.
Oblicz 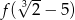 jeżeli
jeżeli 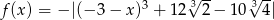 .
.
Wyznacz dziedzinę funkcji
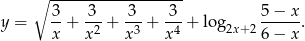
Wielomian 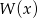 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 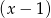 ,
, 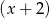 ,
, 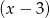 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 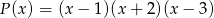 .
.
Funkcja 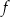 jest określona wzorem
jest określona wzorem
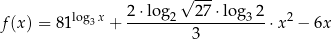
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 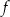 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 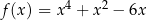 .
. -
Oblicz najmniejszą wartość funkcji
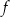 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Funkcja 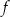 jest określona wzorem
jest określona wzorem
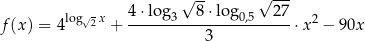
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 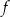 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 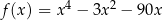 .
. -
Oblicz najmniejszą wartość funkcji
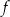 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Wyznacz wzór funkcji 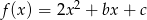 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 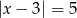 .
.
Wyznacz wzór funkcji 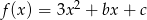 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 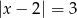 .
.
Oblicz możliwe wartości wyrażenia 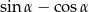 wiedząc, że
wiedząc, że 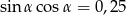 .
.
Wyznacz punkty wspólne wykresów 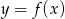 i
i 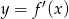 jeżeli
jeżeli 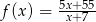 .
.
Wyznacz punkty wspólne wykresów 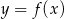 i
i 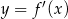 jeżeli
jeżeli 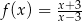 .
.
Reszta z dzielenia wielomianu 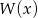 przez wielomian
przez wielomian 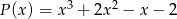 jest równa
jest równa 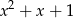 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 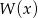 przez wielomian
przez wielomian 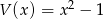 .
.
Dany jest wielomian 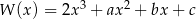 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 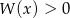 jest zbiór
jest zbiór 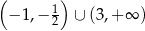 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 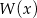 przez dwumian
przez dwumian 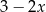 .
.
Kąt  jest ostry i
jest ostry i 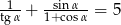 . Oblicz
. Oblicz 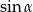 .
.
Wyznacz wartość funkcji 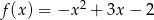 dla argumentu
dla argumentu 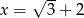 .
.
Wyznacz wartość funkcji 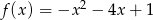 dla
dla 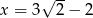 .
.
Wyznacz ekstrema lokalne funkcji 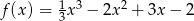 .
.

