Funkcja 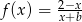 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 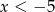 lub
lub 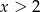 .
.
- Oblicz
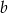 .
. - Napisz wzór funkcji
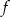 w postaci kanonicznej.
w postaci kanonicznej. - Wyznacz zbiór tych argumentów, dla których funkcja
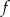 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 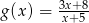 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja 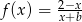 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 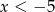 lub
lub 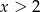 .
.
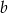 .
. 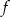 w postaci kanonicznej.
w postaci kanonicznej. 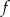 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 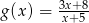 .
.Wyznacz dziedzinę i zbiór wartości funkcji
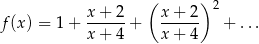
Naszkicuj wykres funkcji 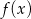 .
.
Oblicz granicę funkcji 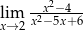 .
.
Oblicz granicę funkcji 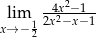 .
.
Określ dziedzinę i zbiór wartości funkcji 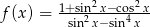 .
.
Reszta z dzielenia wielomianu 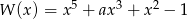 przez dwumian
przez dwumian 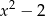 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Wyznacz wzór funkcji liniowej 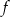 , która dla każdego
, która dla każdego 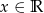 spełnia warunek
spełnia warunek 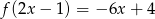 .
.
Wielomian 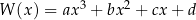 jest iloczynem wielomianów
jest iloczynem wielomianów 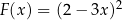 oraz
oraz 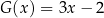 . Oblicz sumę
. Oblicz sumę 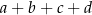 współczynników wielomianu
współczynników wielomianu 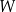 .
.
Funkcja homograficzna 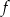 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 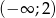 i
i 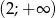 . Zbiór
. Zbiór 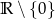 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
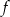 .
. 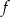 .
. 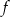 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 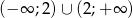 .
.Wielomian 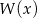 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 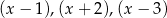 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 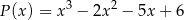 .
.
Przy dzieleniu wielomianu 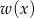 przez dwumian
przez dwumian 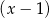 otrzymujemy resztę
otrzymujemy resztę 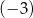 , przy dzieleniu przez dwumian
, przy dzieleniu przez dwumian 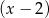 resztę 6, a przy dzieleniu przez dwumian
resztę 6, a przy dzieleniu przez dwumian 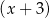 resztę 1. Wyznacz resztę z dzielenia wielomianu
resztę 1. Wyznacz resztę z dzielenia wielomianu 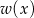 przez wielomian
przez wielomian 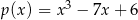 .
.
Wyznacz resztę 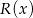 z dzielenia wielomianu
z dzielenia wielomianu 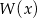 przez wielomian
przez wielomian 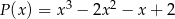 wiedząc, że
wiedząc, że 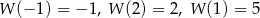 .
.
Reszta z dzielenia wielomianu 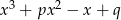 przez trójmian
przez trójmian 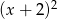 wynosi
wynosi 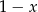 . Wyznacz pierwiastki tego wielomianu.
. Wyznacz pierwiastki tego wielomianu.
Wykaż, że jeżeli 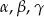 są kątami ostrymi i
są kątami ostrymi i 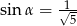 ,
, 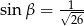 ,
, 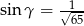 to
to 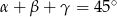 .
.
Funkcja kwadratowa 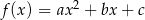 , spełnia warunek
, spełnia warunek 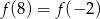 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  , spełniony jest warunek
, spełniony jest warunek 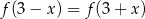 .
.
Wykaż, że jeżeli  i
i 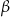 są kątami ostrymi, dla których
są kątami ostrymi, dla których 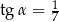 i
i 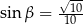 , to
, to 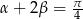 .
.
Oblicz granicę 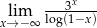 .
.
Oblicz granicę 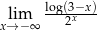 .
.
Wielomian 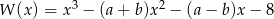 jest podzielny przez dwumian
jest podzielny przez dwumian 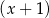 , a reszta z dzielenia wielomianu
, a reszta z dzielenia wielomianu 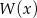 przez dwumian
przez dwumian 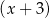 wynosi
wynosi 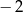 . Oblicz
. Oblicz  i
i 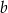 , a następnie rozwiąż nierówność
, a następnie rozwiąż nierówność 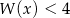 .
.
Funkcja 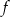 jest określona wzorem
jest określona wzorem 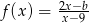 dla
dla 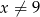 . Ponadto wiemy, że
. Ponadto wiemy, że 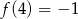 . Oblicz współczynnik
. Oblicz współczynnik 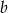 .
.
Wyznacz wszystkie wartości parametru 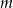 , dla których dziedziną funkcji
, dla których dziedziną funkcji
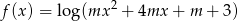
jest zbiór wszystkich liczb rzeczywistych.
Wykaż, że 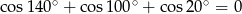 .
.
Kąt  jest taki, że
jest taki, że 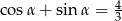 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 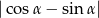 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 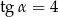 . Wyznacz sinus i cosinus tego kąta.
. Wyznacz sinus i cosinus tego kąta.
Kąt  jest ostry i
jest ostry i 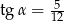 . Oblicz
. Oblicz 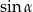 .
.
Kąt  jest ostry i
jest ostry i 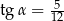 . Oblicz
. Oblicz 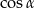 .
.
