Funkcja 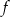 jest określona wzorem
jest określona wzorem 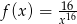 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 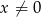 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 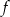 w punkcie
w punkcie 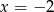 .
.
/Szkoła średnia/Funkcje
Wykaż, że jeżeli wielomian 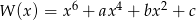 jest podzielny przez trójmian
jest podzielny przez trójmian 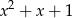 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 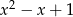 .
.
Wielomian 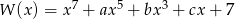 jest podzielny przez wielomian
jest podzielny przez wielomian 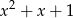 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 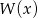 przez wielomian
przez wielomian 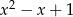 .
.
Wielomian 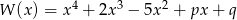 jest podzielny przez dwumian
jest podzielny przez dwumian 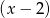 , a przy dzieleniu przez
, a przy dzieleniu przez 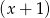 daje resztę
daje resztę 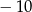 . Wyznacz
. Wyznacz 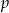 i
i 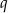 .
.
Wielomian 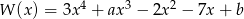 jest podzielny przez dwumian
jest podzielny przez dwumian 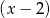 , a przy dzieleniu przez
, a przy dzieleniu przez 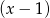 daje resztę 3. Wyznacz
daje resztę 3. Wyznacz  i
i 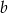 .
.
Uzasadnij, że nie istnieje granica 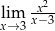 .
.
Określ dziedzinę funkcji 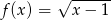 .
.
Wyznacz najmniejszą i największą wartość funkcji 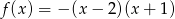 w przedziale
w przedziale 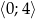 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 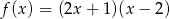 w przedziale
w przedziale 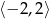 .
.
Wyznacz najmniejszą i największą wartość funkcji 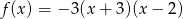 w przedziale
w przedziale 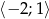 .
.
Wyznacz najmniejszą i największą wartość funkcji 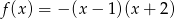 w przedziale
w przedziale 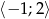 .
.
Wyznacz zbiór wartości funkcji
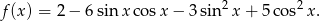
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego  jeżeli
jeżeli 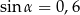 .
.
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego  jeżeli
jeżeli 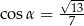 .
.
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 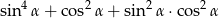 jest stała.
jest stała.
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 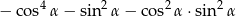 jest stała.
jest stała.
Wykaż, że dla dowolnego kąta  ,
,
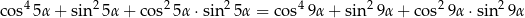
Wyznacz zbiór wartości funkcji 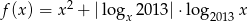 .
.
Dany jest trójmian kwadratowy 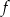 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 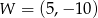 . Oblicz
. Oblicz 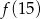 .
.
Określ dziedzinę funkcji 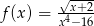 .
.
Funkcja kwadratowa 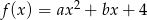 , osiąga wartości ujemne wtedy i tylko wtedy, gdy
, osiąga wartości ujemne wtedy i tylko wtedy, gdy 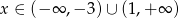 .
.
- Wyznacz wartości współczynników
 i
i 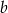 .
. - Napisz postać kanoniczną funkcji
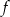 .
. - Podaj wzór funkcji kwadratowej
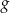 , której wykres otrzymamy przesuwając wykres funkcji
, której wykres otrzymamy przesuwając wykres funkcji 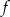 o wektor
o wektor ![→ u = [2,− 130]](https://img.zadania.info/zad/9353293/HzadT7x.gif) .
. - Wyznacz te argumenty
 , dla których
, dla których 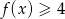 .
.
Wyznacz resztę z dzielenia wielomianu 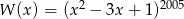 przez wielomian
przez wielomian 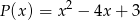 .
.
Funkcja 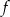 określona jest wzorem
określona jest wzorem 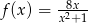 .
.
- Wykaż, że funkcja
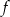 jest nieparzysta.
jest nieparzysta. - Wykaż (z definicji), że funkcja
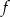 w przedziale
w przedziale 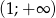 jest malejąca.
jest malejąca. - Wykaż, że funkcja
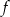 nie przyjmuje wartości większych od 4.
nie przyjmuje wartości większych od 4.
Funkcja 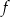 określona jest wzorem
określona jest wzorem
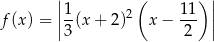
dla każdego 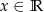 . Pochodna funkcji
. Pochodna funkcji 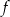 w punkcie
w punkcie 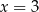 jest równa 0. Wyznacz wszystkie wartości parametru
jest równa 0. Wyznacz wszystkie wartości parametru 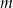 , dla których równanie
, dla których równanie 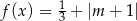 ma cztery rozwiązania, których iloczyn jest ujemny.
ma cztery rozwiązania, których iloczyn jest ujemny.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 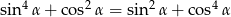 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 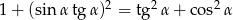 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 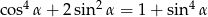 .
.
Wielomian 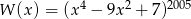 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 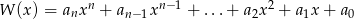 . Oblicz sumę
. Oblicz sumę 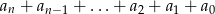 .
.
Wielomian 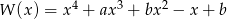 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 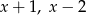 i
i 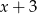 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 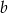 .
.
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 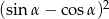 .
.
Dany jest kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 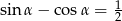 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 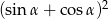 .
.

