Dwa okręgi o środkach 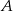 i
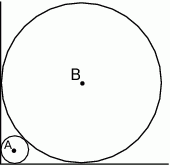
i 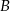 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy 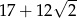 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dwa okręgi o środkach 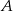 i
i 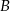 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy 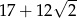 .
.

Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 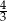 .
.
Dany jest okrąg 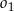 . Kreślimy cięciwę
. Kreślimy cięciwę 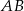 nieprzechodzącą przez środek okręgu
nieprzechodzącą przez środek okręgu 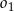 , a następnie rysujemy okrąg
, a następnie rysujemy okrąg 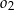 współśrodkowy z okręgiem
współśrodkowy z okręgiem 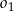 i styczny do cięciwy
i styczny do cięciwy 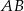 . Okręgi
. Okręgi 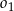 i
i 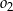 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu
ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu 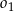 (zależy tylko od długości cięciwy
(zależy tylko od długości cięciwy 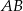 ).
).
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego okręgu (zobacz rysunek).
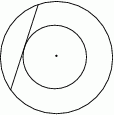
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
