Przez punkt 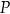 krawędzi bocznej
krawędzi bocznej 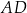 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 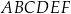 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 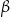 (zobacz rysunek).
(zobacz rysunek).
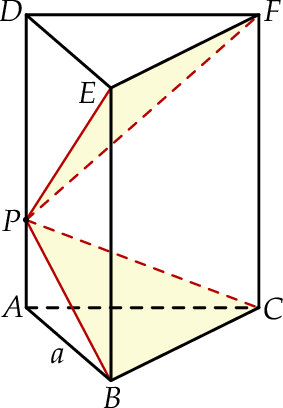
Udowodnij, że objętość ostrosłupa 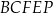 jest równa
jest równa
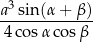

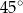 .
. 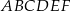 jest trójkąt
jest trójkąt 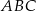 , w którym
, w którym 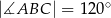 oraz
oraz 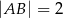 (zobacz rysunek). Trójkąt
(zobacz rysunek). Trójkąt 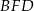 jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa. 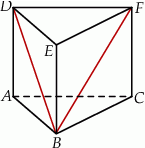
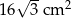 , a pole prostokąta jest równe
, a pole prostokąta jest równe 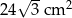 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 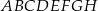 jest romb o boku długości 5, polu 24 i kącie ostrym
jest romb o boku długości 5, polu 24 i kącie ostrym 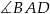 . Graniastosłup ten przecięto płaszczyzną
. Graniastosłup ten przecięto płaszczyzną 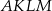 w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym
w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym 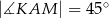 (zobacz rysunek). Oblicz pole tego przekroju.
(zobacz rysunek). Oblicz pole tego przekroju. 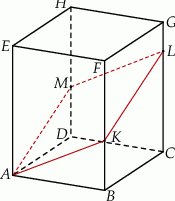
 wyraża się wzorem
wyraża się wzorem 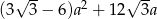 . Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.
. Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa. 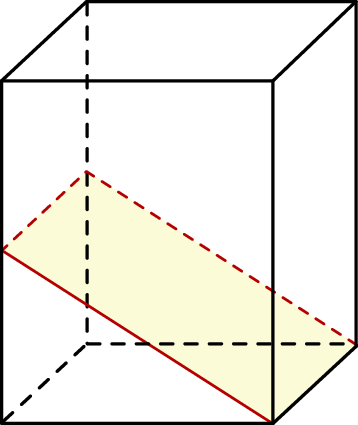
 wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna  z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze
z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze 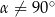 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę  jest równe
jest równe 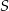 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa. 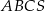 jest trójkąt prostokątny
jest trójkąt prostokątny 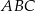 , w którym
, w którym 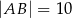 . Stosunek długości przyprostokątnej
. Stosunek długości przyprostokątnej 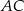 tego trójkąta do długości przyprostokątnej
tego trójkąta do długości przyprostokątnej 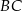 jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.
jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa. 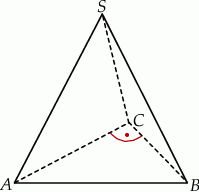
 . Oblicz długość krawędzi podstawy tego graniastosłupa.
. Oblicz długość krawędzi podstawy tego graniastosłupa.  ma długość 4 (zobacz rysunek).
ma długość 4 (zobacz rysunek). 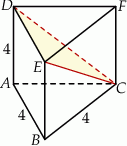
 tego graniastosłupa od płaszczyzny
tego graniastosłupa od płaszczyzny  .
. 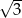 . Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa.
. Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa. 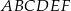 , którego podstawą jest trójkąt
, którego podstawą jest trójkąt 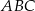 o kątach
o kątach 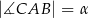 i
i 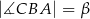 . Przekątne
. Przekątne 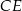 i
i 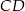 ścian bocznych tworzą kąt o mierze
ścian bocznych tworzą kąt o mierze 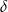 takiej, że
takiej, że 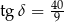 (zobacz rysunek).
(zobacz rysunek). 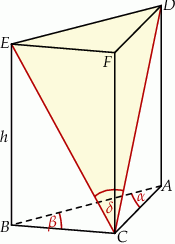
 jest równe 4, a pole trójkąta
jest równe 4, a pole trójkąta  jest równe
jest równe 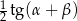 . Oblicz wysokość
. Oblicz wysokość 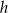 tego graniastosłupa.
tego graniastosłupa.  jest trójkąt równoramienny
jest trójkąt równoramienny  , w którym
, w którym 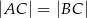 ,
, 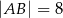 . Wysokość trójkąta
. Wysokość trójkąta 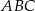 , poprowadzona z wierzchołka
, poprowadzona z wierzchołka 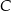 , ma długość 3. Przekątna
, ma długość 3. Przekątna 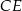 ściany bocznej tworzy z krawędzią
ściany bocznej tworzy z krawędzią 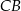 podstawy
podstawy 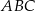 kąt
kąt 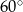 (zobacz rysunek).
(zobacz rysunek). 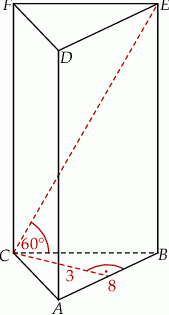
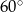 . Wiedząc, że objętość tego graniastosłupa jest równa
. Wiedząc, że objętość tego graniastosłupa jest równa 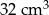 , oblicz pole powierzchni całkowitej tej bryły.
, oblicz pole powierzchni całkowitej tej bryły. 