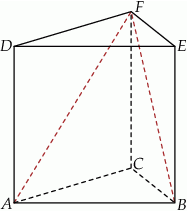
Dany jest graniastosłup prawidłowy trójkątny  . Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
. Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
Oblicz sinus kąta 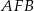 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest graniastosłup prawidłowy trójkątny  . Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
. Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).

Oblicz sinus kąta 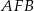 .
.
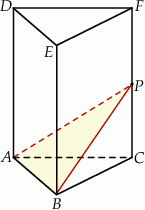
Dany jest graniastosłup prawidłowy trójkątny 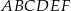 o podstawach
o podstawach 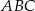 i
i 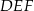 i krawędziach bocznych
i krawędziach bocznych 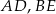 i
i 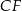 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 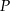 jest środkiem krawędzi
jest środkiem krawędzi 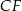 . Długość krawędzi podstawy
. Długość krawędzi podstawy 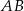 jest równa 12, a pole trójkąta
jest równa 12, a pole trójkąta 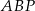 jest równe
jest równe 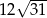 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
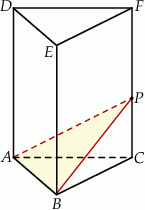
Krawędź podstawy graniastosłupa prawidłowego trójkątnego 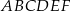 jest równa 6 (zobacz rysunek). Punkt
jest równa 6 (zobacz rysunek). Punkt 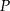 dzieli krawędź boczną
dzieli krawędź boczną 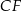 w stosunku
w stosunku 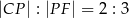 . Pole trójkąta
. Pole trójkąta 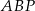 jest równe
jest równe 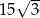 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
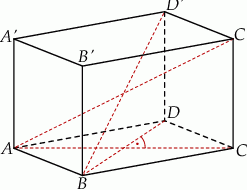
Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, z których żadne dwie nie leżą w jednej płaszczyźnie, i otrzymano trójkąt 
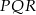 .
. 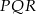 .
.Z czterech ołowianych sześcianów o przekątnej długości 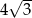 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
Dany jest graniastosłup prosty o podstawie pięciokątnej 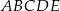 (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta  . Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
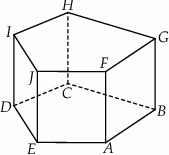
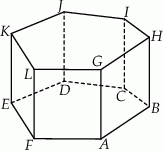
Dany jest graniastosłup prosty o podstawie sześciokątnej  (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta  . Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 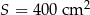 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 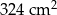 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły .
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż 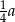 .
.
Dany jest graniastosłup prawidłowy trójkątny 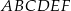 o podstawach
o podstawach 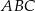 i
i 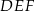 , w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy
, w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy 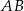 jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy
jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy 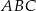 tego graniastosłupa pod takim kątem
tego graniastosłupa pod takim kątem  , że
, że 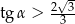 .
.
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem  do dolnej podstawy. Pole otrzymanego przekroju wynosi
do dolnej podstawy. Pole otrzymanego przekroju wynosi 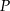 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
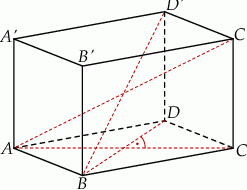
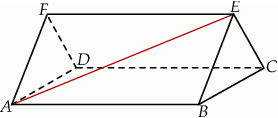
Dany jest graniastosłup prosty 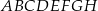 , którego podstawą jest prostokąt
, którego podstawą jest prostokąt 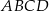 . W tym graniastosłupie
. W tym graniastosłupie 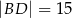 , a ponadto
, a ponadto 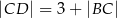 oraz
oraz 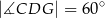 (zobacz rysunek).
(zobacz rysunek).
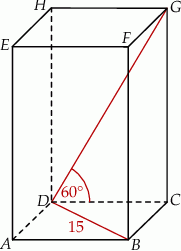
Oblicz objętość i pole powierzchni bocznej tego graniastosłupa.
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
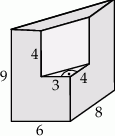
Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 10 cm, oblicz jego pole powierzchni całkowitej.
Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 20 cm, oblicz jego pole powierzchni całkowitej.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 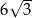 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 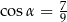 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 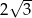 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 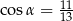 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Podstawą graniastosłupa prostego 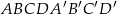 jest romb
jest romb 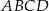 . Przekątna
. Przekątna 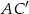 tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 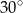 , a przekątna
, a przekątna 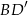 jest nachylona do tej płaszczyzny pod kątem
jest nachylona do tej płaszczyzny pod kątem 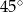 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Podstawą graniastosłupa prostego  jest romb
jest romb  . Przekątna
. Przekątna  tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 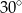 , a objętość graniastosłupa jest równa
, a objętość graniastosłupa jest równa 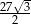 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Podstawą graniastosłupa prostego 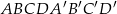 jest romb
jest romb 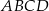 . Przekątna
. Przekątna 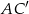 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 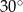 , a przekątna
, a przekątna 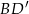 ma długość
ma długość 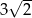 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 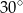 .
.
W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość 4, a przekątna 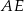 , ściany
, ściany 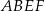 jest nachylona do ściany
jest nachylona do ściany 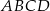 pod kątem ostrym
pod kątem ostrym  takim, że
takim, że 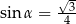 .
.
 .
. Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
Każda krawędź graniastosłupa trójkątnego ma długość 26. Ściana boczna 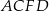 jest prostopadła do płaszczyzny podstawy
jest prostopadła do płaszczyzny podstawy 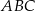 , a krawędź
, a krawędź 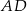 jest nachylona do płaszczyzny podstawy pod katem
jest nachylona do płaszczyzny podstawy pod katem  takim, że
takim, że 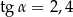 (zobacz rysunek).
(zobacz rysunek).
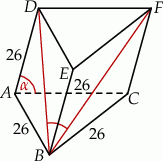
Oblicz cosinus kąta  .
.
Dany jest graniastosłup prawidłowy trójkątny  o podstawach
o podstawach  i
i 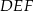 i krawędziach bocznych
i krawędziach bocznych 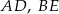 i
i 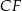 . Oblicz pole trójkąta
. Oblicz pole trójkąta 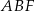 wiedząc, że
wiedząc, że 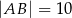 i
i 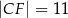 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 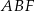 .
.
Dany jest graniastosłup prawidłowy trójkątny 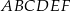 o podstawach
o podstawach 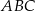 i
i 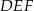 i krawędziach bocznych
i krawędziach bocznych 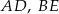 i
i 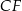 . Oblicz pole trójkąta
. Oblicz pole trójkąta 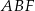 wiedząc, że
wiedząc, że 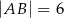 i
i 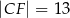 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 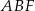 .
.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa.
Podstawą graniastosłupa prostego 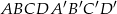 jest równoległobok
jest równoległobok 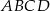 o bokach długości
o bokach długości 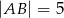 i
i 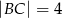 . Oblicz długość wysokości
. Oblicz długość wysokości 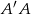 graniastosłupa jeżeli
graniastosłupa jeżeli 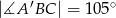 oraz
oraz 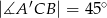 .
.
