Graniastosłup/Stereometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Graniastosłup prawidłowy trójkątny o krawędzi podstawy 4 cm i wysokości 10 cm przecięto płaszczyzną zawierającą wysokość podstawy i jedną z krawędzi bocznych. Jakie pole ma ten przekrój?

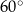Każda ściana graniastosłupa jest rombem o boku długości i kącie ostrym o mierze 60∘ . Oblicz objętość tego graniastosłupa.

Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5 cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.

Ukryj Podobne zadania

Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 4 cm, zaś najdłuższa przekątna graniastosłupa jest 5 razy dłuższa od najkrótszej przekątnej podstawy.

W graniastosłupie prawidłowym sześciokątnym 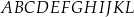ABCDEF GHIJKL płaszczyzna 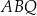ABQ przechodzi przez krawędź 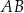i przez środek 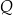krawędzi 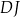(zobacz rysunek).

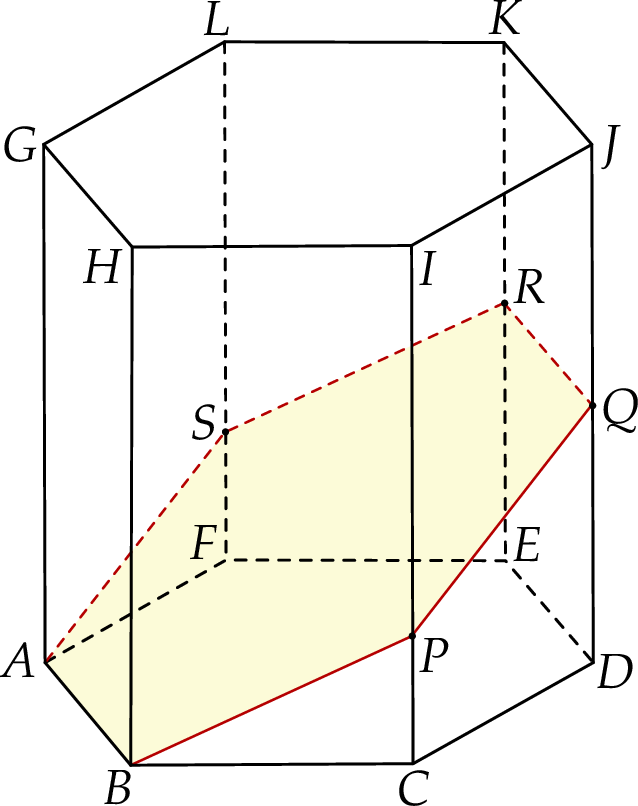
ZINFO-FIGURE

Stosunek pola przekroju graniastosłupa płaszczyzną 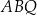ABQ do pola jego podstawy jest równy 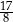178 . Oblicz objętość graniastosłupa 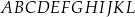ABCDEF GHIJKL , jeżeli jego krawędź boczna ma długość .

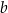Podstawą graniastosłupa prostego 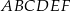ABCDEF jest trójkąt prostokątny 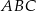ABC , w którym 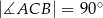|∡ACB | = 9 0∘ (zobacz rysunek). Stosunek długości przyprostokątnej 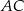tego trójkąta do długości przyprostokątnej 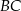jest równy 4:3. Punkt 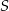jest środkiem okręgu opisanego na trójkącie 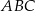ABC , a długość odcinka 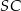jest równa 5. Pole ściany bocznej 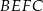BEF C graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.

Ukryj Podobne zadania

Podstawą graniastosłupa prostego 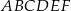ABCDEF jest trójkąt prostokątny 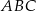ABC , w którym 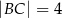|BC | = 4 . Promień okręgu opisanego na trójkącie 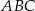ABC ma długość 3, a sinus kąta nachylenia przekątnej 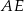ściany bocznej 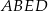ABED do płaszczyzny podstawy jest równy 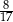-8 17 . Oblicz objętość tego graniastosłupa.

Graniastosłup prawidłowy czworokątny o krawędzi podstawy 6 cm przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne i jest nachylona do płaszczyzny podstawy pod kątem 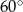60 ∘ . Zaznacz na rysunku ten przekrój i oblicz jego pole.

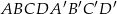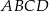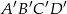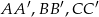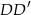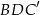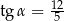Dany jest graniastosłup prawidłowy czworokątny ′ ′ ′ ′ ABCDA B C D o podstawach ABCD i A ′B ′C ′D ′ , oraz krawędziach bocznych AA ′,BB ′,CC ′ i DD ′ . Oblicz pole trójkąta BDC ′ wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem , że 12 tg α = 5 .

Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość 12 cm, a wysokość graniastosłupa jest równa 8 cm. Oblicz pole przekroju graniastosłupa płaszczyzną wyznaczoną przez krawędź podstawy i środek przeciwległej krawędzi bocznej.

Ukryj Podobne zadania

Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość 6 cm, a wysokość graniastosłupa jest równa 10 cm. Oblicz pole przekroju graniastosłupa płaszczyzną wyznaczoną przez krawędź podstawy i środek przeciwległej krawędzi bocznej.

Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe 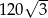√ -- 12 0 3 , a pole jego powierzchni całkowitej wynosi 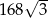√ -- 168 3 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.

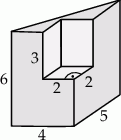
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.

Ukryj Podobne zadania

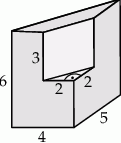
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.

W graniastosłupie prawidłowym czworokątnym przekątne ścian bocznych, wychodzące z tego samego wierzchołka, mają długość 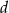i tworzą kąt o mierze . Oblicz objętość tego graniastosłupa.

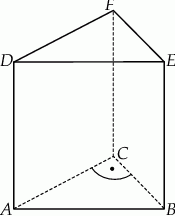
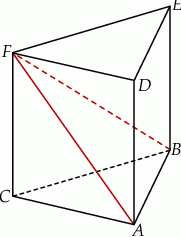
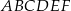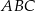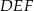Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych 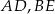AD ,BE i 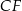(zobacz rysunek). Długość krawędzi podstawy 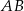jest równa 8, a pole trójkąta 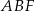ABF jest równe 52. Oblicz objętość tego graniastosłupa.

Podstawą graniastosłupa prostego jest trójkąt 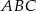ABC o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.

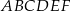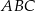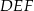Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych 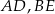AD ,BE i 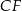(zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 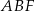ABF poprowadzoną z wierzchołka 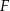i płaszczyzną podstawy 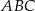ABC tego graniastosłupa jest równy 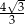4√3 -3-- . Oblicz pole trójkąta ABF .

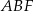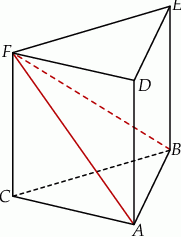
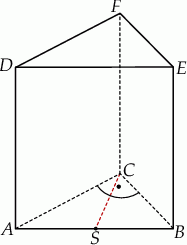
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem 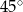45 ∘ do dolnej podstawy. Pole otrzymanego przekroju wynosi 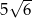√ -- 5 6 . Oblicz objętość tego graniastosłupa.

W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 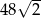√ -- 48 2 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy 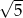√ -- 5 . Oblicz objętość tego graniastosłupa.

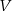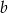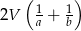Podstawą graniastosłupa prostego o objętości jest równoległobok o bokach długości i . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż ( ) 2V 1 + 1 a b .

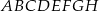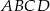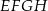Dany jest graniastosłup czworokątny prosty ABCDEF GH o podstawach ABCD i EF GH oraz krawędziach bocznych 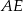, , 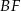, 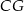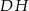. Podstawa 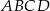ABCD graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych 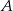i 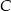o mierze 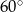60 ∘ . Przekątna graniastosłupa 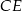jest nachylona do płaszczyzny podstawy pod kątem 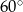∘ 6 0 . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.

Ukryj Podobne zadania

W graniastosłupie prostym o podstawie rombu krótsza przekątna podstawy ma długość 6 cm i tworzy z krawędzią podstawy kąt 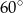60 ∘ . Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 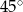45∘ . Oblicz objętość graniastosłupa.

Podstawą graniastosłupa prostego jest romb. Krótsza przekątna rombu tworzy z krawędzią podstawy kąt 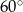60∘ i ma długość 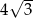√ -- 4 3 . Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt 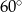6 0∘ . Oblicz objętość graniastosłupa.

Podstawą graniastosłupa prostego 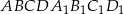ABCDA 1B1C1D 1 jest trapez równoramienny 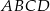ABCD wpisany w okrąg o środku 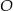i promieniu 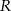. Dłuższa podstawa 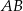trapezu jest średnicą tego okręgu, a krótsza ma długość (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze . Wyznacz objętość tego graniastosłupa jako funkcję promienia 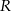, długości podstawy i miary kąta .

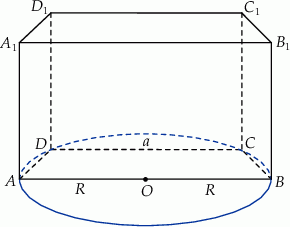
Krótsza przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 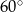6 0∘ . Przekątna ściany bocznej ma długość √ --- 4 10 .

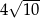Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
Oblicz cosinus kąta między krótszymi przekątnymi graniastosłupa wychodzącymi z jednego wierzchołka.

Strona 3 z 6