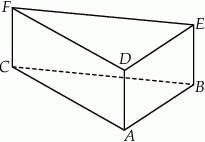
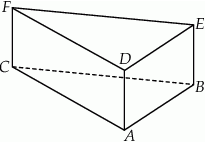
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 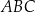 zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem
zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 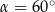 . Pole przekroju graniastosłupa tą płaszczyzną równa się
. Pole przekroju graniastosłupa tą płaszczyzną równa się 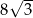 . Zaznacz na poniższym rysunku kąt
. Zaznacz na poniższym rysunku kąt  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
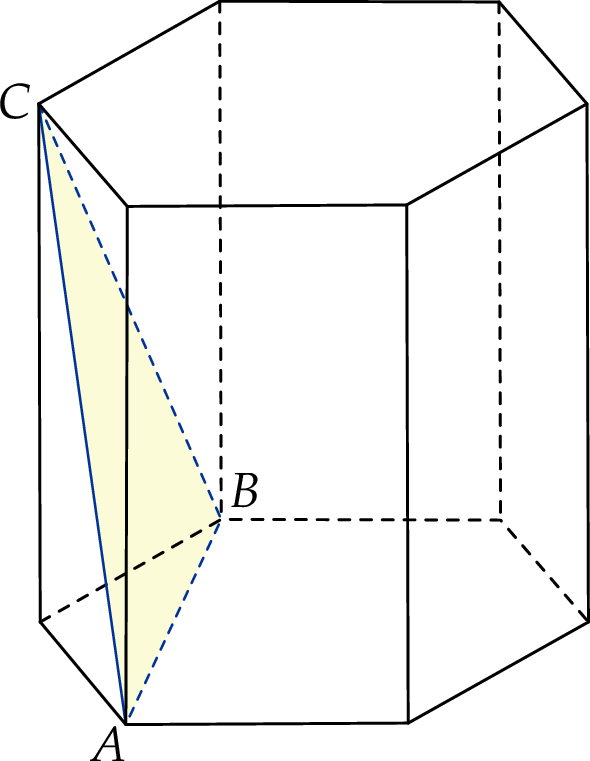

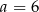 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 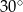 . Oblicz
. Oblicz 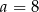 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 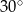 . Oblicz
. Oblicz  i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 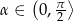 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.  i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 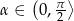 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki. 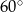 oblicz pole otrzymanego przekroju.
oblicz pole otrzymanego przekroju. 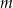 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem  . Wiadomo, że
. Wiadomo, że 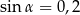 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  , taki że
, taki że 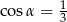 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 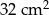 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  , taki że
, taki że 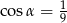 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 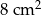 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  takim, że
takim, że 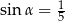 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  takim, że
takim, że 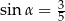 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. 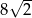 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 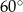 . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
. Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek. 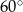 . Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu.
. Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu. 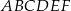 o podstawach
o podstawach 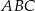 i
i 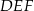 i krawędziach bocznych
i krawędziach bocznych 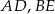 i
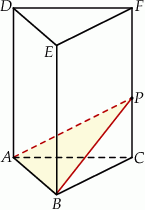
i 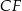 (zobacz rysunek). Przez krawędź
(zobacz rysunek). Przez krawędź 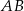 poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem
poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem 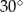 . Płaszczyzna ta przecina krawędź
. Płaszczyzna ta przecina krawędź 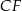 w punkcie
w punkcie 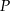 . Oblicz pole trójkąta
. Oblicz pole trójkąta 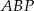 jeżeli objętość ostrosłupa
jeżeli objętość ostrosłupa 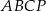 jest równa
jest równa 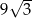 .
. 
 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem  (zobacz rysunek).
(zobacz rysunek). 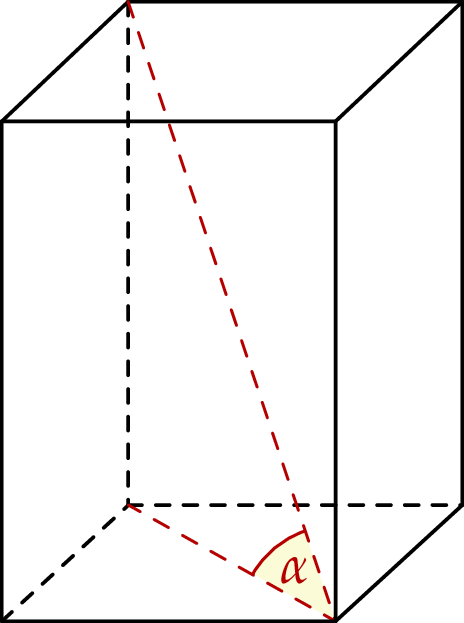
 oraz pole powierzchni całkowitej tego graniastosłupa.
oraz pole powierzchni całkowitej tego graniastosłupa.  o podstawach
o podstawach  i
i 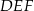 i krawędziach bocznych
i krawędziach bocznych 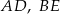 i
i 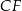 , które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta
, które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta 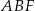 stanowi
stanowi 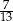 pola ściany bocznej
pola ściany bocznej 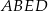 .
. 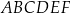 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 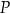 . Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka
. Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka 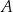 ma miarę
ma miarę 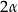 . Objętość tego graniastosłupa jest równa
. Objętość tego graniastosłupa jest równa 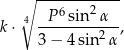
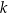 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 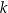 .
. 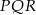
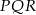 .
. 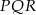 .
. . Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.
. Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa. 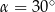 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 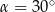 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 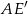 graniastosłupa prawidłowego sześciokątnego ma długość
graniastosłupa prawidłowego sześciokątnego ma długość 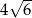 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 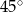 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 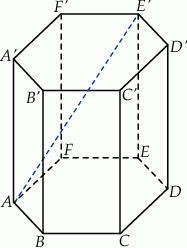
 , a kąt ostry miarę
, a kąt ostry miarę 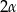 . Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi
. Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi 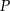 . Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
. Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój. 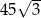 . Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.