W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 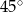 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 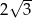 .
.
/Szkoła średnia/Geometria/Stereometria/Graniastosłup
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 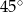 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 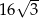 .
.
Długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa  . Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka
. Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka 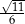 . Wyznacz pole powierzchni całkowitej tego graniastosłupa.
. Wyznacz pole powierzchni całkowitej tego graniastosłupa.
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, przechodzącą przez jeden punkt z wierzchołków podstawy, otrzymując w przekroju romb o kącie ostrym  . Wyznacz
. Wyznacz 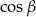 , gdzie
, gdzie 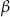 jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły.
jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły.
Podstawą graniastosłupa prostego 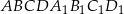 jest trapez równoramienny
jest trapez równoramienny 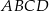 wpisany w okrąg o środku
wpisany w okrąg o środku 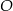 i promieniu
i promieniu 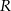 . Dłuższa podstawa
. Dłuższa podstawa 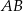 trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze
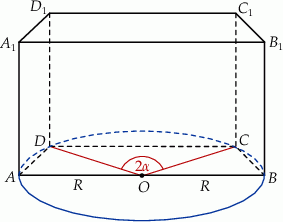
trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 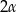 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 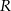 i miary kąta
i miary kąta  .
.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 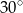 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 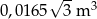 . Oblicz objętości obu pojemników.
. Oblicz objętości obu pojemników.
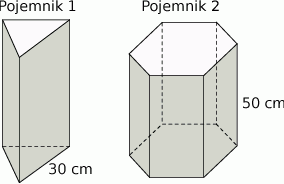
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 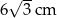 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 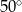 . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
. Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
W graniastosłupie prawidłowym czworokątnym 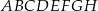 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 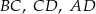 i
i 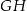 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 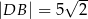 i kąt
i kąt 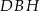 ma miarę
ma miarę 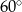 .
.
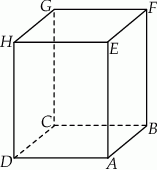
Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 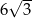 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość 5 cm, a krawędź boczna ma długość 4 cm. Przez wierzchołek górnej podstawy i przekątną dolnej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju. Rozpatrz 2 przypadki.
Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 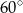 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 6. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 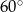 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
Promień okręgu opisanego na podstawie graniastosłupa prawidłowego trójkątnego ma długość 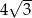 . Pole powierzchni bocznej jest równe 144.
. Pole powierzchni bocznej jest równe 144.
- Oblicz objętość tego graniastosłupa.
- Oblicz cosinus kąta między przekątną ściany bocznej i krawędzią podstawy graniastosłupa.
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
Dany jest graniastosłup prawidłowy trójkątny o podstawach 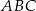 i
i 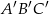 oraz krawędziach bocznych
oraz krawędziach bocznych 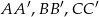 . Kąt nachylenia przekątnej ściany bocznej
. Kąt nachylenia przekątnej ściany bocznej 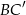 do płaszczyzny podstawy ma miarę
do płaszczyzny podstawy ma miarę  . Promień okręgu wpisanego w podstawę graniastosłupa ma długość
. Promień okręgu wpisanego w podstawę graniastosłupa ma długość  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 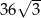 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 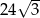 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Dany jest graniastosłup, którego podstawą jest równoległobok o polu 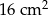 i kącie ostrym
i kącie ostrym 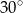 . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe
. Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 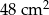 i
i 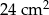 .
.
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy  i wysokości
i wysokości 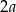 . Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 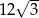 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 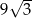 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.

