Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Prawdopodobieństwo

Wyszukiwanie zadań

Liczby ze zbioru 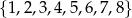{1,2,3,4,5,6,7,8 } ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie:
– cyfra 1 stoi na lewo od cyfry 2,
– cyfra 3 stoi na lewo od cyfry 4,
– cyfra 5 stoi na lewo od cyfry 6,
– cyfra 7 stoi na lewo od cyfry 8?
Uwaga, w powyższych warunkach nie zakładamy, że odpowiednie cyfry stoją obok siebie, np. liczba 13275846 spełnia wszystkie powyższe warunki.

Wybieramy losowo 2 kostki z tabliczki czekolady przedstawionej na poniższym rysunku.

PIC

Oblicz prawdopodobieństwo tego, że wybrane dwie kostki są sąsiednie (tzn. mają wspólną krawędź).

W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 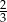2 3 ?

Z talii 52 kart losujemy jednocześnie dwie karty. Oblicz prawdopodobieństwo, że przynajmniej jedna z nich będzie starsza od 10, jeśli wiadomo, że żadna z nich nie jest karem.

Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.

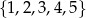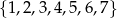Dane są zbiory liczb całkowitych: {1,2,3,4 ,5 } i {1,2,3,4 ,5,6,7} . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.

Ukryj Podobne zadania

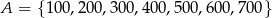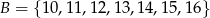Dane są dwa zbiory: A = {10 0,200,300,4 00,500,600 ,700} i B = {10,1 1,12,13,14,1 5,16} . Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.

Dane są dwa zbiory:

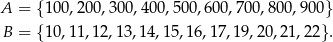
A = {10 0,200,300,4 00,500,600 ,700,800,90 0} B = {10 ,1 1,12,13,14,1 5,16,17,19,2 0,21,22}.

Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 9.

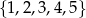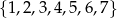Dane są zbiory liczb całkowitych: {1,2,3,4 ,5 } i {1,2,3,4 ,5,6,7} . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 7.

Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.

Rzucamy 5 razy symetryczną monetą. Oblicz prawdopodobieństwo otrzymania co najmniej 4 orłów lub co najmniej 4 reszek, jeżeli wiadomo, że otrzymaliśmy co najmniej jedną reszkę.

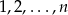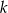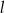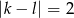Ze zbioru 1,2,...,n losujemy kolejno bez zwracania 2 liczby k i l . Dla jakich wartości n prawdopodobieństwo tego, że |k− l| = 2 jest większe od 14 ?

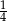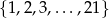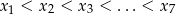Ze zbioru liczb {1,2 ,3 ,...,21} losujemy jednocześnie siedem liczb i ustawiamy je w kolejności rosnącej x1 < x2 < x 3 < ...< x 7 . Oblicz prawdopodobieństwo zdarzenia x2 ≤ 3 .

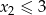Ze zbioru liczb 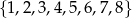{1,2,3,4 ,5,6,7,8} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 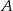A , polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.

Ukryj Podobne zadania

Ze zbioru liczb 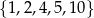{1,2 ,4 ,5,10} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 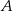A polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.

Ze zbioru liczb 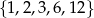{1,2 ,3 ,6,12} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 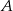A polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.

Ze zbioru ośmioelementowego 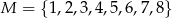M = {1,2,3,4 ,5 ,6,7,8} losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 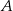A polega na wylosowaniu dwóch liczb ze zbioru 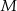M , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia A .

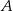Ze zbioru dziewięcioelementowego 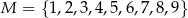M = { 1,2,3,4,5,6,7,8,9 } losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 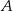A polega na wylosowaniu dwóch liczb ze zbioru 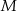M , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia A .

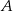Dwaj równorzędni przeciwnicy grają w szachy. Co jest bardziej prawdopodobne:

  • wygranie dwóch partii z trzech, czy czterech partii z sześciu rozegranych?
  • wygranie nie mniej niż dwóch partii z trzech, czy nie mniej niż czterech partii z sześciu rozegranych? (Remisów nie uwzględniamy.)

W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.

Ukryj Podobne zadania

W pudełku jest 7 kul białych i 3 czarne. Doświadczenie polega na wylosowaniu 3 kul. Jakie jest prawdopodobieństwo wylosowania co najwyżej dwóch kul białych?

Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg arytmetyczny.

Ukryj Podobne zadania

Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg geometryczny.

Strona 22 z 22