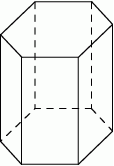
Sześcian, którego ściany zostały pomalowane czerwoną farbą, dzielimy 6 płaszczyznami równoległymi do jego ścian na 27 identycznych sześcianików. Losujemy 2 spośród nich.
- Oblicz prawdopodobieństwo, że łączna liczba czerwonych ścian wylosowanych sześcianików wynosi 3.
- Oblicz prawdopodobieństwo, że wylosowane sześcianiki mają wspólną ścianę.

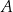 polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych. 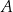 polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.  polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych. 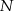 losów, przy czym
losów, przy czym 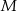 z nich to losy wygrywające (
z nich to losy wygrywające (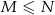 ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (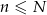 ) i niech
) i niech 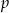 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 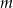 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (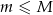 oraz
oraz 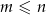 ). Uzasadnij, że
). Uzasadnij, że 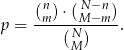
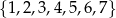 losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą. 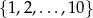 losujemy dwie różne liczby
losujemy dwie różne liczby  i
i 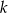 . Oblicz prawdopodobieństwo, że
. Oblicz prawdopodobieństwo, że 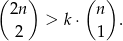
 kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 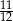 . Oblicz
. Oblicz  .
.  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 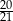 . Oblicz
. Oblicz  .
. 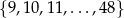 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. 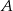 i
i 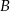 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 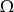 , że
, że 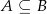 oraz
oraz 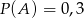 i
i 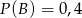 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 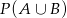 .
.