Prawdopodobieństwo/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo

W dwóch pudełkach umieszczono po pięć kul, przy czym w pierwszym pudełku: 2 kule białe i 3 kule czerwone, a w drugim pudełku: 1 kulę białą i 4 kule czerwone. Z pierwszego pudełka losujemy jedną kulę i bez oglądania wkładamy ją do drugiego pudełka. Następnie losujemy jedną kulę z drugiego pudełka. Oblicz prawdopodobieństwo wylosowania kuli białej z drugiego pudełka.

Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.

Gracz 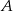rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz 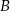rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza .

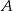Oblicz prawdopodobieństwo, że w czterech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 5.

Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.

Ukryj Podobne zadania

Z urny, w której jest 7 kul czarnych i 3 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.

Z urny, w której jest 5 kul czerwonych i 7 czarnych wyjęto dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wyjęto kule w różnych kolorach.

Z urny, w której jest 6 kul czarnych i 2 zielone, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.

Spośród liczb dwucyfrowych wybrano bez zwracania dwa razy po jednej liczbie. Oblicz prawdopodobieństwo, że dwa razy wybrano liczbę parzystą.

Ukryj Podobne zadania

Spośród dodatnich liczb dwucyfrowych losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo wylosowania dwóch liczb parzystych.

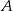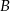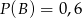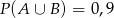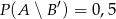O zdarzeniach i wiadomo, że P (B) = 0,6 , P(A ∪ B) = 0 ,9 oraz P (A ∖ B′) = 0,5 . Oblicz prawdopodobieństwo zdarzenia .

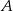W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 1000 do 9999. Każdy los, którego numer jest liczbą o sumie cyfr równej 3, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.

Ukryj Podobne zadania

W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 2000 do 7000. Każdy los, którego numer jest liczbą o sumie cyfr równej 4, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.

Wybieramy trzy karty z talii 24 kart, składającej się ze wszystkich ﬁgur oraz dziewiątek i dziesiątek. Jakie jest prawdopodobieństwo że wszystkie wylosowane karty to kiery.

Ukryj Podobne zadania

Wybieramy trzy karty z talii 24 kart, składającej się ze wszystkich ﬁgur oraz dziewiątek i dziesiątek. Jakie jest prawdopodobieństwo, że wśród tych kart jest co najmniej jeden as.

Wybieramy trzy karty z talii 24 kart, składającej się ze wszystkich ﬁgur oraz dziewiątek i dziesiątek. Jakie jest prawdopodobieństwo, że wśród tych kart jest jedna ﬁgura.

W pewnym przedsiębiorstwie 9% wyrobów jest brakami. Na 100 dobrych wyrobów 70 jest pierwszego gatunku. Jakie jest prawdopodobieństwo, że wylosowany wyrób jest pierwszego gatunku?

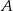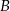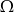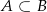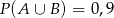Zdarzenia losowe i są zawarte w przestrzeni . Wiedząc, że A ⊂ B oraz P (A ∪ B ) = 0,9 , oblicz P(B ′) .

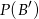Mamy trzy pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, w drugim – 4 kule ponumerowane kolejnymi liczbami od 1 do 4, a w trzecim – 5 kul ponumerowanych kolejnymi liczbami od 1 do 5. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę trzycyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą setek, numer kuli wylosowanej z drugiego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z trzeciego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 4.

Klasy IIIa i IIIb liczą odpowiednio 10 dziewcząt i 18 chłopców oraz 16 dziewcząt i 12 chłopców. Wybieramy losowo jedną z tych dwóch klas i losujemy z niej jednego ucznia. Jakie jest prawdopodobieństwo wylosowania dziewczynki?

W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.

Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?

Ze zbioru liczb 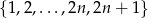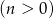{1,2,...,2n ,2n + 1} , (n > 0) , losujemy jednocześnie dwie liczby. Niech 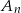oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.

Dany jest zbiór wszystkich dwucyfrowych liczb naturalnych. Oblicz prawdopodobieństwo, że losowo wybrana z tego zbioru liczba jest podzielna przez 6 lub przez 8.

Ukryj Podobne zadania

Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 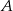polegającego na tym, że otrzymamy liczbę podzielną przez 8 lub liczbę podzielną przez 12.

Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 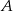polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub liczbę podzielną przez 12.

Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 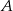polegającego na tym, że otrzymamy liczbę podzielną przez 6 lub liczbę podzielną przez 9.

Ze zbioru liczb 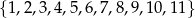{1,2,3,4 ,5,6,7,8,9,10,11 } wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 3 lub przez 2.

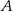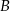O zdarzeniach i wiadomo, że 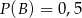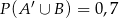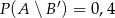P (B) = 0,5 ; ′ P (A ∪ B) = 0,7 ; P (A ∖ B′) = 0,4 . Oblicz prawdopodobieństwo zdarzenia A ∪ B .

Ukryj Podobne zadania

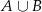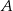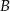O zdarzeniach i wiadomo, że 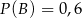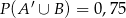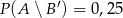P (B) = 0,6 ; ′ P (A ∪ B) = 0,75 ; P (A ∖ B′) = 0,25 . Oblicz prawdopodobieństwo zdarzenia A ∪ B .

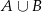W pojemniku ze słodyczami znajduje się 48 cukierków i 32 lizaki. Osiem lizaków i piętnaście cukierków ma smak jabłkowy, a pozostałe słodycze mają smak pomarańczowy. Z pojemnika wybrano losowo jeden słodycz (cukierek lub lizak) i okazało się, że ma smak pomarańczowy. Oblicz prawdopodobieństwo zdarzenia, że wybrany słodycz jest lizakiem.

Na trzech loteriach kupiono po jednym losie. Prawdopodobieństwo wygrania na pierwszej loterii wynosi 50%, na drugiej 60%, a na trzeciej 70%. Jakie jest prawdopodobieństwo:

wygrania na trzech loteriach;
niewygrania na żadnej;
wygrania przynajmniej na jednej loterii.

Strona 20 z 22