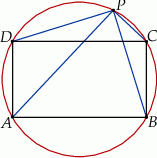
Punkt 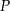 należy do okręgu opisanego na prostokącie
należy do okręgu opisanego na prostokącie 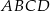 . Wykaż, że
. Wykaż, że 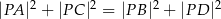 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt 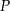 należy do okręgu opisanego na prostokącie
należy do okręgu opisanego na prostokącie 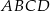 . Wykaż, że
. Wykaż, że 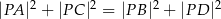 .
.

Punkt 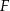 jest środkiem boku
jest środkiem boku 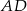 prostokąta
prostokąta 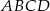 , w którym
, w którym 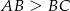 . Punkt
. Punkt 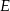 jest takim punktem boku
jest takim punktem boku 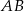 tego prostokąta, że prosta
tego prostokąta, że prosta 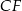 jest dwusieczną kąta
jest dwusieczną kąta 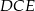 . Wykaż, że trójkąt
. Wykaż, że trójkąt 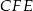 jest prostokątny.
jest prostokątny.
Dwa prostokąty podobne mają obwody równe odpowiednio 21 cm i 7 cm, a pole większego wynosi 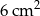 . Oblicz pole mniejszego prostokąta.
. Oblicz pole mniejszego prostokąta.
W prostokącie 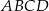 punkt
punkt 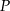 jest środkiem boku
jest środkiem boku 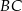 , a punkt
, a punkt 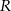 jest środkiem boku
jest środkiem boku 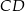 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 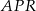 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 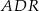 oraz
oraz 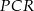 .
.
W prostokącie 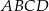 punkt
punkt 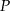 jest środkiem boku
jest środkiem boku 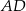 , a punkt
, a punkt 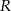 jest środkiem boku
jest środkiem boku 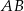 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 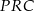 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 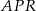 oraz
oraz 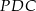 .
.
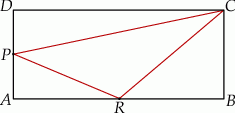
Dany jest prostokąt 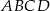 , w którym
, w którym 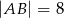 i
i 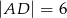 . Na boku
. Na boku 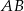 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 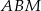 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta  .
.
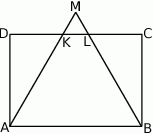
W prostokącie 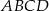 połączono wierzchołki
połączono wierzchołki 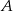 i
i 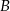 ze środkiem boku
ze środkiem boku 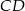 i otrzymano trójkąt, którego jeden z kątów ma miarę
i otrzymano trójkąt, którego jeden z kątów ma miarę 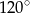 . Wiedząc, że
. Wiedząc, że 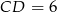 oblicz obwód prostokąta
oblicz obwód prostokąta 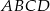 .
.
Dany jest prostokąt 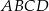 , w którym
, w którym 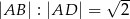 . Punkt
. Punkt 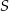 jest środkiem boku
jest środkiem boku 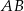 . Oblicz miarę kąta między prostymi
. Oblicz miarę kąta między prostymi 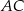 i
i 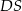 .
.
Prostokąt jest wpisany w okrąg o promieniu 10, a jego dłuższe boki są styczne do okręgu o promieniu 3.
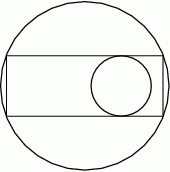
Oblicz pole tego prostokąta.
Prostokąt 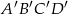 jest podobny do prostokąta
jest podobny do prostokąta 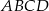 w skali
w skali 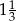 . Pole prostokąta
. Pole prostokąta 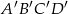 jest równe
jest równe 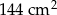 . Krótszy bok prostokąta
. Krótszy bok prostokąta 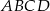 ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
Prostokąt 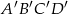 jest podobny do prostokąta
jest podobny do prostokąta 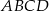 w skali
w skali 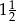 . Pole prostokąta
. Pole prostokąta 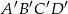 jest równe
jest równe 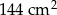 . Krótszy bok prostokąta
. Krótszy bok prostokąta 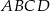 ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
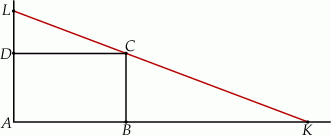
Przez wierzchołek 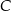 prostokąta
prostokąta 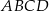 poprowadzono prostą, która przecięła proste
poprowadzono prostą, która przecięła proste 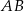 i
i 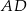 w punktach
w punktach 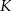 i
i 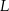 odpowiednio. Wykaż, że
odpowiednio. Wykaż, że 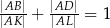 .
.
Uzasadnij, że jeżeli prostokąt 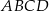 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

Na boku 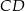 prostokąta
prostokąta 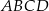 wybrano punkt
wybrano punkt 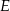 taki, że
taki, że 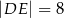 . Przekątna
. Przekątna 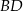 i odcinek
i odcinek 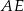 przecinają się w punkcie
przecinają się w punkcie 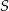 oraz
oraz 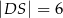 . Bok
. Bok 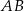 prostokąta
prostokąta 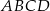 ma długość 12 (zobacz rysunek).
ma długość 12 (zobacz rysunek).
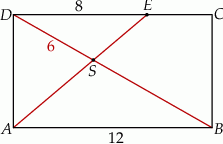
Oblicz długość odcinka 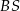 .
.
Boki prostokąta 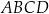 mają długości 5 i 12. Oblicz odległość wierzchołka
mają długości 5 i 12. Oblicz odległość wierzchołka 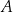 od przekątnej
od przekątnej 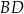 .
.
W wyniku zwiększenia każdego boku danego prostokąta o 2 cm jego pole wzrosło o 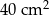 . O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
. O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
W wyniku zwiększenia każdego boku danego prostokąta o 2 cm jego pole wzrosło o 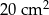 . O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
. O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
Niech 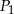 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 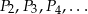 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
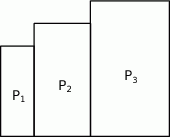
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 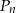 jest równy 246.
jest równy 246.
Dany jest prostokąt o bokach  i
i 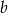 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 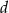 . Długość boku
. Długość boku  to 90% długości boku
to 90% długości boku  . Długość boku
. Długość boku 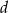 to 120% długości boku
to 120% długości boku 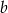 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 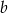 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 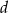 .
.
Dany jest prostokąt o bokach  i
i 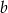 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 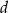 . Długość boku
. Długość boku  to 80% długości boku
to 80% długości boku  . Długość boku
. Długość boku 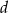 to 140% długości boku
to 140% długości boku 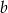 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 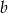 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 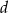 .
.
Podaj wymiary prostokąta, którego boki różnią się o 6 cm, a przekątna ma długość 30 cm.
W prostokącie połączono środki sąsiednich boków. Powstały w ten sposób romb ma obwód 40 cm i pole równe 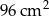 . Oblicz długości boków prostokąta.
. Oblicz długości boków prostokąta.
W trójkąt równoramienny o ramieniu 10 i podstawie 12 wpisano prostokąt o stosunku boków 1:4 w ten sposób, ze krótszy bok jest zawarty w podstawie trójkąta. Oblicz długości boków prostokąta.
Niech 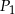 będzie prostokątem o polu
będzie prostokątem o polu 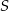 i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty
i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty 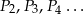 podobne do prostokąta
podobne do prostokąta 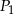 takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów
takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów 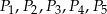 .
.
