Dany jest prostokąt  . Z wierzchołków
. Z wierzchołków  i
i  poprowadzono proste prostopadłe do przekątnej
poprowadzono proste prostopadłe do przekątnej 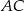 dzielące ją na trzy odcinki
dzielące ją na trzy odcinki 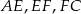 , każdy długości 4. Oblicz długość boków prostokąta.
, każdy długości 4. Oblicz długość boków prostokąta.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt
Punkt 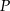 leży wewnątrz prostokąta
leży wewnątrz prostokąta 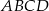 . Wykaż, że suma pól trójkątów
. Wykaż, że suma pól trójkątów 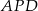 i
i 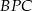 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 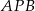 i
i 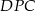 .
.
Długości boków prostokąta są równe 3 oraz 5. Oblicz sinus kąta ostrego, który tworzą przekątne tego prostokąta.
Długości boków prostokąta są równe 8 oraz 15. Oblicz cosinus kąta rozwartego, który tworzą przekątne tego prostokąta.
W prostokącie przekątna o długości 1,53 cm tworzy z dłuższym bokiem kąt o mierze 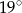 . Oblicz z dokładnością do
. Oblicz z dokładnością do 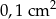 pole prostokąta.
pole prostokąta.
Wyznacz pole narysowanego prostokąta, jeżeli 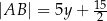 .
.
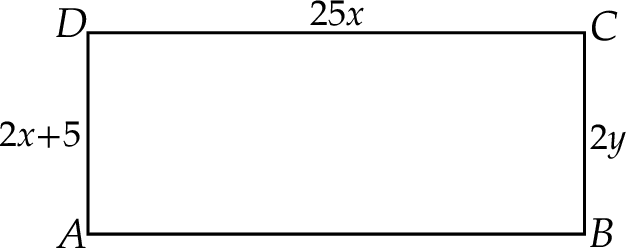
O ile centymetrów należy przedłużyć długość i szerokość prostokąta o wymiarach 8 cm na 5 cm aby jego pole zwiększyło się o 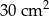 ?
?
Boki prostokąta 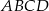 mają długości
mają długości 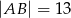 i
i 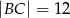 . Punkt
. Punkt 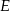 jest punktem boku
jest punktem boku 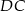 takim, że
takim, że 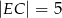 , a punkt
, a punkt 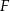 jest takim punktem odcinka
jest takim punktem odcinka 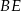 , że
, że 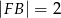 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 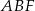 .
.
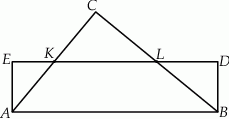
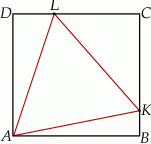
W prostokąt 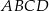 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 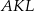 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 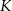 leży na boku
leży na boku 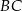 (
(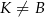 i
i 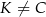 ), wierzchołek
), wierzchołek 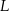 leży na boku
leży na boku 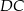 (
(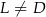 i
i 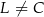 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 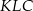 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 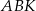 i
i 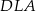 .
.
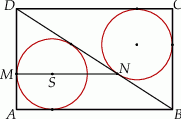
Dany jest prostokąt 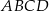 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 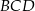 jest styczny do przekątnej
jest styczny do przekątnej 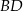 w punkcie
w punkcie 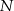 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 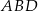 jest styczny do boku
jest styczny do boku 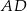 w punkcie
w punkcie 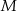 , a środek
, a środek 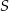 tego okręgu leży na odcinku
tego okręgu leży na odcinku 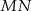 , jak na rysunku.
, jak na rysunku.
Wykaż, że 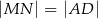 .
.
Sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy 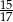 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
Odcinek 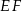 łączący środki dwóch dłuższych boków prostokąta
łączący środki dwóch dłuższych boków prostokąta 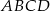 dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta
dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta 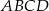 .
.
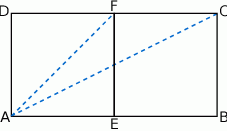
Pole prostokąta jest równe 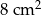 . Wyznacz jeden z boków prostokąta, jako funkcję drugiego boku i naszkicuj wykres tej funkcji. Podaj dziedzinę i zbiór wartości tej funkcji.
. Wyznacz jeden z boków prostokąta, jako funkcję drugiego boku i naszkicuj wykres tej funkcji. Podaj dziedzinę i zbiór wartości tej funkcji.
Dany jest prostokąt 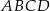 . Na boku
. Na boku 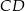 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 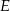 , że
, że 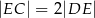 , a na boku
, a na boku 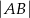 wybrano taki punkt
wybrano taki punkt 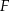 , że
, że 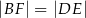 . Niech
. Niech 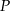 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 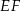 z prostą
z prostą 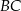 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 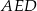 i
i 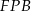 są przystające.
są przystające.
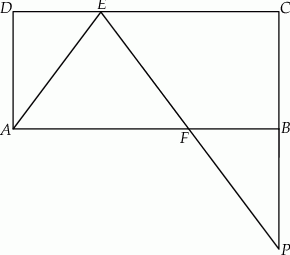
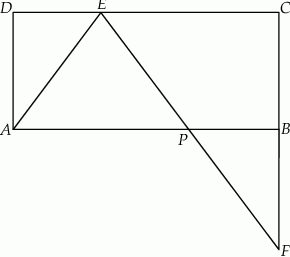
Dany jest prostokąt 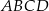 . Na boku
. Na boku 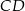 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 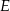 , że
, że 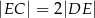 , a na przedłużeniu boku
, a na przedłużeniu boku 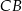 wybrano taki punkt
wybrano taki punkt 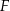 , że
, że 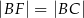 . Niech
. Niech 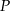 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 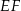 z prostą
z prostą 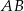 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 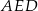 i
i 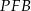 są przystające.
są przystające.
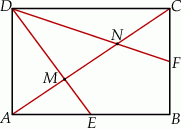
W prostokącie 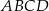 wierzchołek
wierzchołek 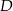 połączono odcinkami ze środkami
połączono odcinkami ze środkami 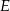 i
i 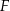 boków
boków 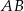 i
i 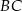 , zaś
, zaś 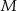 i
i 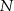 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 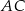 .
.
- Uzasadnij, że odcinki
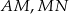 i
i 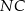 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
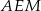 i
i 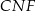 mają równe pola.
mają równe pola.
Długości boków prostokąta 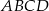 są równe:
są równe: 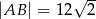 i
i 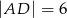 . Na odcinku
. Na odcinku 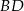 wybrano punkt
wybrano punkt 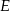 w ten sposób, że
w ten sposób, że 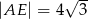 . Oblicz długość odcinka
. Oblicz długość odcinka 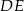 .
.
W prostokącie 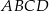 , w którym
, w którym 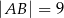 ,
, 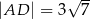 , na przekątnej
, na przekątnej 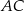 wybrano taki punkt
wybrano taki punkt 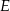 , że
, że 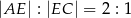 . Oblicz sinus kąta
. Oblicz sinus kąta 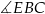 .
.
W prostokącie 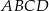 , w którym
, w którym 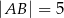 ,
, 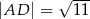 , na przekątnej
, na przekątnej 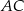 wybrano taki punkt
wybrano taki punkt 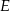 , że
, że 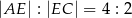 . Oblicz sinus kąta
. Oblicz sinus kąta 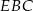 .
.
Przekątne prostokąta mają długość 20 cm i przecinają się pod kątem 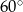 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
Oblicz pole prostokąta, którego przekątna ma długość 7 cm, a jeden z boków ma długość 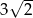 cm.
cm.
Na bokach 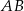 i
i 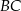 prostokąta
prostokąta 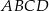 wybrano punkty
wybrano punkty 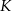 i
i 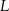 w ten sposób, że trójkąt
w ten sposób, że trójkąt 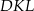 jest ostrokątny oraz
jest ostrokątny oraz 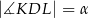 . Odcinek
. Odcinek 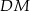 jest wysokością trójkąta
jest wysokością trójkąta 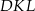 .
.
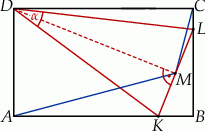
Wykaż, że 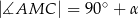 .
.
Na rysunku przedstawiono prostokąt 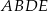 i trójkąt
i trójkąt 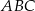 . Punkty
. Punkty 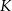 i
i 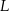 dzielą odcinki
dzielą odcinki 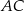 i
i 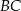 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 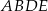 jest równe polu trójkąta
jest równe polu trójkąta 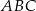 .
.