Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 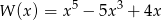 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
/Szkoła średnia/Funkcje/Wielomiany
Wielomian 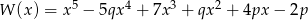 jest podzielny przez wielomian
jest podzielny przez wielomian 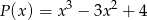 . Wyznacz
. Wyznacz 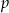 i
i 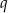 .
.
Wyznacz wartości  i
i 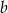 współczynników wielomianu
współczynników wielomianu 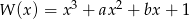 wiedząc, że
wiedząc, że 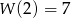 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 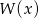 przez
przez 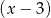 jest równa 10.
jest równa 10.
Jednym z pierwiastków wielomianu 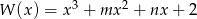 jest liczba 1. Reszta z dzielenia wielomianu
jest liczba 1. Reszta z dzielenia wielomianu 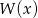 przez dwumian
przez dwumian 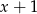 jest równa 4. Oblicz współczynniki
jest równa 4. Oblicz współczynniki 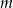 i
i  .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Reszty z dzielenia wielomianu 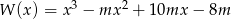 przez dwumiany
przez dwumiany 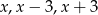 są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru
są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru 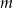 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Sprawdź, czy równe są wielomiany 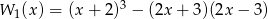 i
i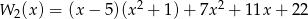 .
.
Reszta z dzielenia wielomianu 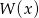 przez wielomian
przez wielomian 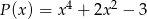 jest wielomianem
jest wielomianem 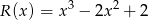 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 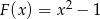 .
.
Wynikiem dzielenia wielomianu 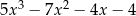 przez dwumian
przez dwumian 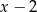 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 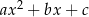 . Oblicz
. Oblicz 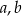 i
i  .
.
Wynikiem dzielenia wielomianu 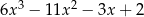 przez dwumian
przez dwumian 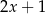 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 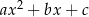 . Oblicz
. Oblicz 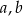 i
i  .
.
W wyniku podzielenia wielomianu 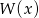 przez
przez 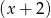 otrzymujemy iloraz
otrzymujemy iloraz 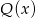 i resztę 0. Jeśli natomiast podzielimy wielomian
i resztę 0. Jeśli natomiast podzielimy wielomian 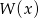 przez
przez 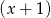 , to otrzymamy iloraz
, to otrzymamy iloraz 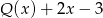 i resztę 2.
i resztę 2.
- Wyznacz wielomian
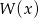 .
. - Rozwiąż nierówność
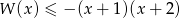 .
.
Wielomian 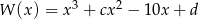 jest podzielny przez dwumian
jest podzielny przez dwumian 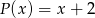 . Przy dzieleniu wielomianu
. Przy dzieleniu wielomianu 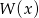 przez dwumian
przez dwumian 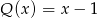 otrzymujemy resztę
otrzymujemy resztę 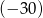 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 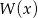 i rozwiąż nierówność
i rozwiąż nierówność 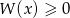 .
.
Wielomian 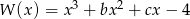 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 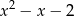 . Wyznacz współczynniki
. Wyznacz współczynniki 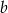 i
i  wielomianu
wielomianu 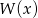 .
.
Wielomian 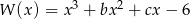 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 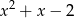 . Wyznacz współczynniki
. Wyznacz współczynniki 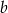 i
i  wielomianu
wielomianu 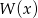 .
.
Dany jest wielomian 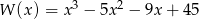 .
.
- Sprawdź, czy punkt
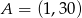 należy do wykresu tego wielomianu.
należy do wykresu tego wielomianu. - Zapisz wielomian
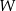 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dla jakiej wartości parametru 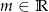 funkcja
funkcja 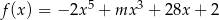 ma ekstremum w punkcie
ma ekstremum w punkcie 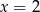 ?
?
Dany jest wielomian 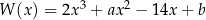 .
.
-
Dla
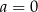 i
i 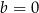 otrzymamy wielomian
otrzymamy wielomian 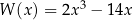 . Rozwiąż równanie
. Rozwiąż równanie 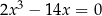 .
. -
Dobierz wartości
 i
i 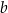 tak, aby wielomian
tak, aby wielomian 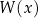 był podzielny jednocześnie przez
był podzielny jednocześnie przez 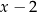 oraz
oraz 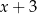 .
.
Wykaż, że jeżeli wielomian 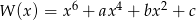 jest podzielny przez trójmian
jest podzielny przez trójmian 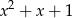 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 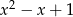 .
.
Wielomian 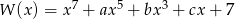 jest podzielny przez wielomian
jest podzielny przez wielomian 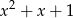 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 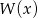 przez wielomian
przez wielomian 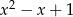 .
.
Wielomian 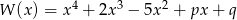 jest podzielny przez dwumian
jest podzielny przez dwumian 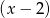 , a przy dzieleniu przez
, a przy dzieleniu przez 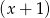 daje resztę
daje resztę 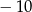 . Wyznacz
. Wyznacz 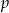 i
i 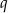 .
.
Wielomian 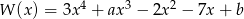 jest podzielny przez dwumian
jest podzielny przez dwumian 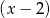 , a przy dzieleniu przez
, a przy dzieleniu przez 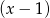 daje resztę 3. Wyznacz
daje resztę 3. Wyznacz  i
i 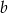 .
.
Wyznacz resztę z dzielenia wielomianu 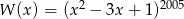 przez wielomian
przez wielomian 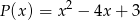 .
.
Wielomian 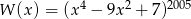 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 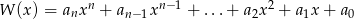 . Oblicz sumę
. Oblicz sumę 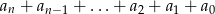 .
.
Wielomian 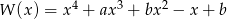 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 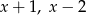 i
i 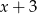 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 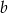 .
.
Reszta z dzielenia wielomianu 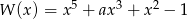 przez dwumian
przez dwumian 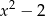 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.

