Za każdy test można otrzymać jedną z ocen: 1, 2, 3, 4, 5 albo 6. Średnia ocen Beaty z czterech testów jest równa 4. Które z poniższych zdań nie może być prawdziwe?
A) Beata otrzymała z każdego testu ocenę 4
B) Beata otrzymała ocenę 3 dokładnie z dwóch testów
C) Beata otrzymała ocenę 1 dokładnie z jednego testu
D) Beata otrzymała ocenę 4 dokładnie z dwóch testów
E) Beata otrzymała ocenę 3 dokładnie z trzech testów.
/Konkursy/Zadania testowe/Zadania z treścią
W sejfie przechowywana jest pewna liczba naszyjników. Wszystkie naszyjniki mają tę samą liczbę pereł (każdy ma ich co najmniej dwie). Liczba wszystkich pereł w tych naszyjnikach jest większa od 200, ale mniejsza od 300. Wiadomo, że znajomość liczby wszystkich pereł w tych naszyjnikach pozwala jednoznacznie określić liczbę tych naszyjników. Ile naszyjników znajduje się w sejfie?
A) 16 B) 17 C) 19 D) 25 E) Inna liczba
Mirek, Mietek i Piotr zbierali pieniądze na zakup namiotu. Mirek dał 60% potrzebnej kwoty, Mietek dał 40% pozostałej części. Piotr dołożył brakujące 30 zł. Ile kosztował namiot?
A) 50 zł B) 60 zł C) 125 zł D) 150 zł E) 200 zł
Państwo Kowalscy mają kilkoro dzieci. Średnia wieku rodziny Kowalskich wynosi 18 lat. Natomiast średnia wieku wszystkich członków rodziny bez ojca, który ma 38 lat, jest równa 14 lat. Ile dzieci jest w rodzinie Kowalskich?
A) 2 B) 3 C) 4 D) 5 E) 6
Arek, Bartek i Cyryl mają razem 30 piłeczek. Gdy Bartek dał 5 piłeczek Cyrylowi, Cyryl dał 4 piłeczki Arkowi, a Arek 2 Bartkowi, to okazało się, że chłopcy mają po tyle samo piłeczek. Ile piłeczek na początku miał Arek?
A) 8 B) 9 C) 11 D) 13 E) 15
Pudełko czekoladek kosztuje 10 zł. W każdym pudełku znajduje się kupon. Za każde trzy kupony możemy otrzymać dodatkowe pudełko czekoladek gratis. Jaka jest największa liczba pudełek czekoladek, które możemy otrzymać za 150 zł.?
A) 15 B) 17 C) 20 D) 21 E) 22
Zegarek babci Jasia spieszy się o jedną minutę w ciągu godziny, a zegarek jego dziadka spóźnia się o jedną minutę w ciągu godziny. Wychodząc po wizycie z domu babci i dziadka, Jasio ustawił na ich zegarkach ten sam czas i powiedział, że odwiedzi ich ponownie, gdy różnica czasu na ich zegarkach będzie wynosiła dokładnie jedną godzinę. Po ilu godzinach Jasio ponownie odwiedzi babcię i dziadka?
A) 12h B) 14h 30min C) 30h D) 60h E) 90h
W pewnej wiosce żadnych dwóch mieszkańców nie ma tej samej liczby włosów na głowie. Żaden z mieszkańców nie ma dokładnie 2007 włosów. Mieszkańcem tej wsi o największej liczbie włosów jest Kargul. Liczba mieszkańców jest większa od liczby włosów na głowie Kargula. W tej wiosce mieszka co najwyżej
A) 0 mieszkańców
B) 2006 mieszkańców
C) 2007 mieszkańców
D) 2008 mieszkańców
E) 2009 mieszkańców
Wiadomo, że jeżeli kangurek Skoczek odbija się lewą nogą, to jego skok ma długość 2 m. Jeżeli odbija się prawą nogą, to skok ma długość 4 m. Gdy Skoczek odbija się obiema nogami, to skacze na odległosć 7 m. Jaką najmniejszą liczbę skoków musi wykonać Skoczek, aby przebyć odległość równą dokładnie 1000 m?
A) 140 B) 144 C) 175 D) 176 E) 150
Wyspę zamieszkują kłamcy i prawdomówni (kłamcy zawsze kłamią, a prawdomówni zawsze mówią prawdę). Pewnego dnia zebrało się 12 wyspiarzy, wśród których byli kłamcy i prawdomówni i wygłosiło kilka stwierdzeń. Dwóch z nich powiedziało: „Dokładnie dwie osoby wśród nas dwunastu to kłamcy”. Każda z następnych czterech osób powiedziała: „Dokładnie cztery osoby wśród nas dwunastu to kłamcy”. Natomiast każda z pozostałych sześciu osób stwierdziła: „Dokładnie sześć osób wśród nas dwunastu to kłamcy". Ilu jest kłamców wśród tej dwunastki wyspiarzy?
A) 2 B) 4 C) 6 D) 8 E) 10
Wyspę zamieszkują prawdomówni i kłamcy. Prawdomówni zawsze mówią prawdę, a kłamcy zawsze kłamią. 25 mieszkańców tej wyspy ustawiło się w kolejkę. Każda osoba z kolejki, z wyjątkiem pierwszej, powiedziała: Osoba stojąca bezpośrednio przede mną to kłamca, natomiast osoba stojąca jako pierwsza w kolejce powiedziała: Wszyscy stojący za mną to kłamcy. Ilu kłamców stało w tej kolejce?
A) 24 B) 13 C) 12 D) 0 E) Nie można obliczyć
W wyniku ankiety przeprowadzonej z udziałem 2006 uczestników stwierdzono, że 1500 spośród nich uczestniczyło w konkursie „Kangur Matematyczny”, a 1200 w konkursie języka angielskiego. Ilu uczestników ankiety brało udział w obydwu konkursach, jeżeli wiadomo, że 6 ankietowanych nie wzięło udziału w żadnym z konkursów?
A) 300 B) 500 C) 600 D) 700 E) 1000
Jacek w ramach przygotowań do konkursu „Kangur Matematyczny” postanowił rozwiązać po jednym zadaniu z kolejnych stron o numerach nieparzystych w swoim zbiorze zadań. Rozpoczął na stronie 15, a skończył na stronie na stronie 53. Ile zadań treningowych rozwiązał Jacek?
A) 19 B) 20 C) 27 D) 38 E) 53
W pokoju bawią się koty i psy. Liczba kocich łap jest dwa razy większa niż liczba psich nosów. Liczba kotów jest
A) dwa razy większa od liczby psów.
B) równa liczbie psów.
C) równa połowie liczby psów.
D)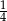 
liczby psów.
E)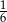 
liczby psów.
Klasa liczy 9 chłopców i 13 dziewcząt. Połowa uczniów tej klasy jest przeziębiona. Co najmniej ile dziewcząt jest przeziębionych?
A) 0 B) 1 C) 2 D) 3 E) 4
Basia buduje z zapałek kolejno układanki zgodnie ze schematem widocznym na rysunku obok, na którym zaznaczono układanki o numerach 1, 2, 3. O ile więcej zapałek zużyła do układanki o numerze 31 niż do układanki o numerze 30?
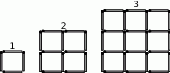
A) 124 B) 148 C) 61 D) 254 E) 120
Nietaktowny mężczyzna zapytał swoją sąsiadkę, ile ma lat. Sąsiadka odpowiedziała mu: „Jeśli będę żyła równa sto lat, to mój obecny wiek stanowi dwie trzecie czasu, jaki mi pozostał do przeżycia.” Ile lat ma sąsiadka?
A) 20 B) 40 C) 50 D) 60 E) 80
Konkurs „Kangur Matematyczny” odbywa się w Europie każdego roku począwszy od 1991. W roku 2006 odbywa się on po raz
A) 15 B) 16 C) 17 D) 13 E) 14
Babcia upiekła swoim wnukom paszteciki. Gdyby dała każdemu z nich po 2, to pozostałyby jej 3 paszteciki, a gdyby chciała dać każdemu z nich po 3, to zabrakłoby jej 2 pasztecików. Ilu wnuków ma babcia?
A) 2 B) 3 C) 4 D) 5 E) 6
W pewnej klasie okazało się, że liczba chłopców, którzy rozwiązali zadania kangurowe, jest równa liczbie dziewcząt, które nie potrafiły tego zadania rozwiązać. Kogo było więcej w tej klasie: tych wszystkich, którzy rozwiązali zadanie, czy wszystkich dziewcząt?
A) Wszystkich dziewcząt
B) Tych wszystkich, którzy rozwiązali zadanie
C) Tych, którzy rozwiązali zadanie, było tyle samo co wszystkich dziewcząt
D) Nie da się tego ustalić
E) Opisana sytuacja jest niemożliwa
