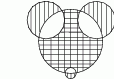
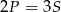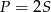Moneta o średnicy 1 cm toczy się po obwodzie sześciokąta foremnego o boku długości 1 cm (patrz rysunek) tak długo, aż powróci do położenia początkowego. Ile centymetrów ma długość drogi, którą zakreślił środek monety?
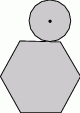
A) 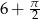 B)
B) 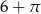 C)
C) 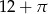 D)
D) 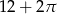 E)
E) 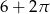

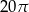
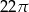
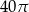
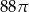
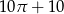
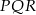 , jeśli
, jeśli 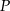 jest wierzchołkiem prostokąta, a
jest wierzchołkiem prostokąta, a 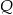 i
i 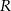 punktami styczności?
punktami styczności? 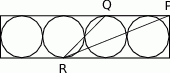
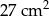
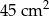
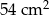
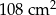
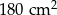
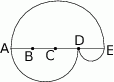
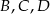 dzielą odcinek
dzielą odcinek 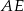 na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio
na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio 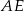 ,
, 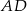 i
i 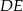 . Jaki jest stosunek długości półokręgu
. Jaki jest stosunek długości półokręgu 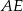 do sumy długości półokręgów
do sumy długości półokręgów 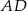 i
i 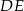 ?
? 
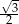


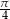
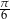

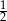
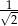
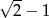
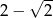

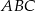 i
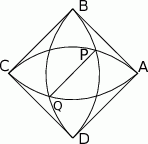
i 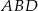 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 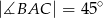 oraz
oraz 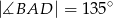 . Wówczas długości cięciw
. Wówczas długości cięciw 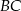 i
i 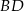 spełniają zależność
spełniają zależność 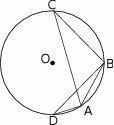
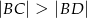
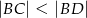
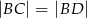
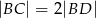
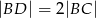
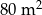 , a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
, a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury? 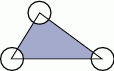
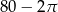
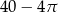
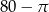
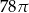
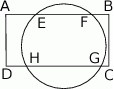
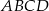 w punktach
w punktach 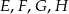 , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 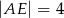 ,
, 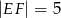 ,
, 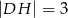 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 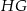 ?
? 
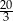
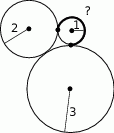
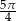
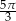
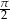
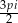
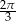
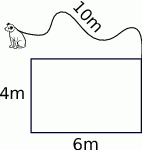
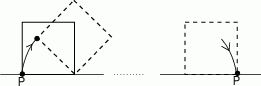
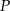 ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt
ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt 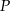 ?
? 
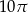
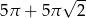
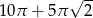
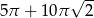
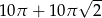
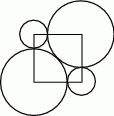
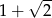
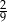
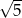
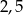
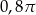
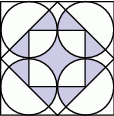
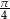
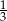
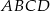 o boku długości 1 oraz łuki okręgów o środkach
o boku długości 1 oraz łuki okręgów o środkach 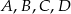 .
. 
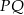 ?
?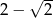

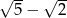
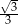
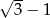
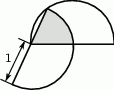
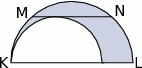
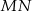 większego półokręgu, która jest równoległa do
większego półokręgu, która jest równoległa do 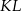 i styczna do mniejszego półokręgu. Ile wynosi pole zacieniowanego obszaru, jeżeli
i styczna do mniejszego półokręgu. Ile wynosi pole zacieniowanego obszaru, jeżeli 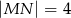 ?
? 
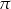
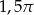
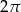
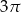
 . Kąt środkowy oparty na łuku długości 2 ma miarę
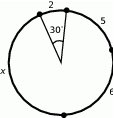
. Kąt środkowy oparty na łuku długości 2 ma miarę 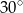 . Jaką wartość ma
. Jaką wartość ma  .
. 
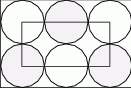
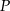 oznacza pole obszaru zakreskowanego liniami pionowymi i niech
oznacza pole obszaru zakreskowanego liniami pionowymi i niech 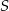 będzie polem zakreskowanej figury. Średnice kół wynoszą odpowiednio 6, 4, 4 i 2. Wówczas
będzie polem zakreskowanej figury. Średnice kół wynoszą odpowiednio 6, 4, 4 i 2. Wówczas