W trójkącie 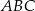 dane są:
dane są: 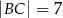 ,
, 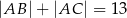 ,
, 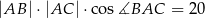 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny
Na bokach 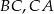 i
i 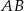 trójkąta
trójkąta 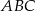 wybrano punkty
wybrano punkty 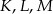 takie, że
takie, że
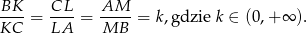
Oblicz stosunek pola trójkąta 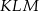 do pola trójkąta
do pola trójkąta 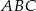 .
.
Suma długości wszystkich wysokości trójkąta 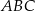 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 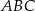 jest równoboczny.
jest równoboczny.
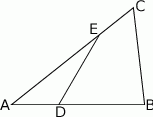
Na bokach 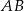 i
i 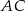 trójkąta
trójkąta 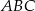 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 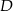 i
i 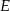 , że
, że 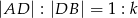 oraz
oraz 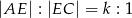 , dla
, dla 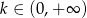 .
.
- Wyznacz wzór funkcji
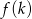 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 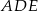 i
i 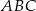 .
. - Wiedząc że
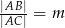 , dla
, dla 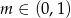 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 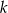 , dla których trójkąty
, dla których trójkąty 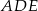 i
i 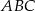 są podobne.
są podobne.
Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 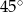 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Punkt 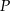 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 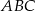 oraz
oraz 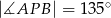 . Wykaż, że trójkąt
. Wykaż, że trójkąt 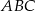 jest prostokątny.
jest prostokątny.
Dwa boki trójkąta wpisanego w okrąg o promieniu 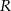 są odpowiednio równe
są odpowiednio równe 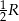 i
i 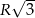 . Oblicz długość trzeciego boku.
. Oblicz długość trzeciego boku.
W trójkącie 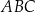 kąt
kąt 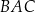 jest dwa razy większy od kąta
jest dwa razy większy od kąta 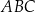 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 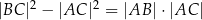 .
.
Dany jest trójkąt 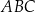 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 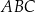 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 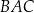 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
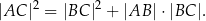
Dany jest trójkąt 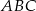 , w którym
, w którym 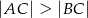 . Na bokach
. Na bokach 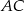 i
i 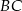 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 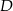 i
i 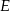 , że
, że 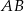 i
i 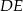 przecinają się w punkcie
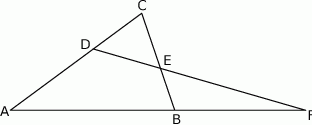
przecinają się w punkcie 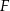 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 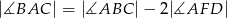 , to
, to 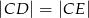 .
.
Jaki warunek musi spełniać liczba  , aby istniał trójkąt o bokach
, aby istniał trójkąt o bokach 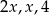 ?
?
Udowodnij, że trzy środkowe rozcinają trójkąt na sześć części o równych polach.
Odcinki 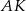 i
i 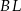 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 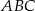 , a punkt
, a punkt 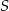 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
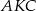 i
i 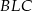 ;
; 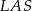 i
i 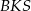 ;
; 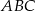 i
i 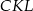 .
.
Odcinki 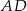 i
i 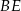 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 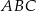 , a punkt
, a punkt 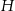 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 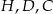 i
i 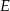 leżą na jednym okręgu.
leżą na jednym okręgu.
Wyznacz wszystkie wartości  , dla których liczby
, dla których liczby 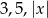 mogą być długościami boków trójkąta.
mogą być długościami boków trójkąta.
W trójkącie 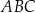 symetralna boku
symetralna boku 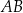 dzieli bok
dzieli bok 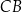 na odcinki długości
na odcinki długości 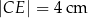 i
i 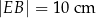 . Bok
. Bok 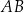 ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość
ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość 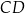 podzieliła bok
podzieliła bok 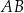 .
.

