W trójkącie 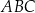 dane są długości dwóch boków
dane są długości dwóch boków 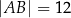 ,
, 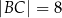 oraz miara kąta
oraz miara kąta 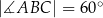 . Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
. Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny
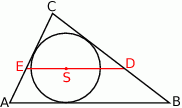
Przez środek 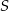 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 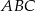 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 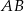 , która przecina boki
, która przecina boki 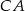 i
i 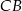 odpowiednio w punktach
odpowiednio w punktach 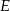 i
i 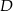 .
.
Wykaż, że 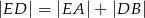 .
.
Dany jest trójkąt o wymiarach 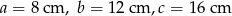 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
Dany jest trójkąt o wymiarach 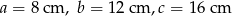 . Oblicz obwód trójkąta podobnego w skali
. Oblicz obwód trójkąta podobnego w skali 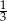 .
.
W trójkącie ostrokątnym 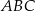 bok
bok 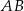 ma długość
ma długość  , długość boku
, długość boku 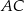 jest równa
jest równa 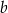 oraz
oraz 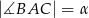 . Dwusieczna kąta
. Dwusieczna kąta 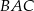 przecina bok
przecina bok 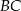 trójkąta w punkcie
trójkąta w punkcie 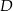 i odcinek
i odcinek 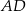 ma długość
ma długość 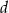 . Wykaż, że
. Wykaż, że
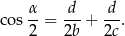
W trójkącie 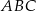 poprowadzono odcinki
poprowadzono odcinki 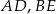 i
i 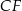 w ten sposób, że punkty
w ten sposób, że punkty 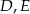 i
i 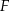 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 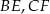 i
i 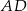 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 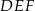 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta 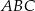 .
.
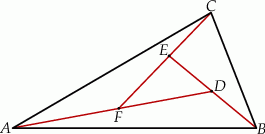
W trójkącie 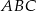 dane są
dane są 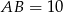 ,
, 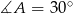 i
i 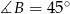 . Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
. Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Oblicz cosinus najmniejszego kąta  trójkąta o bokach 2 cm, 4 cm, 5 cm.
trójkąta o bokach 2 cm, 4 cm, 5 cm.
Dany jest trójkąt 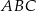 o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
Dany jest trójkąt 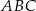 o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
Na bokach trójkąta 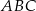 zbudowano kwadraty
zbudowano kwadraty 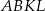 ,
, 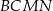 i
i 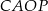 (zobacz rysunek).
(zobacz rysunek).
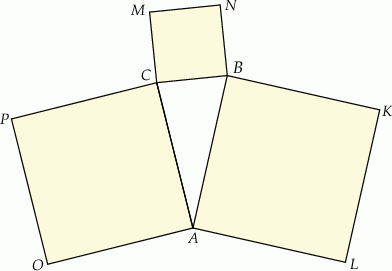
Kąty 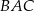 i
i 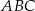 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 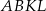 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 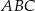 , to suma pól kwadratów
, to suma pól kwadratów 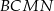 i
i 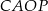 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta 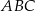 .
.
W trójkącie 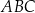 środkowa
środkowa 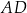 jest prostopadła do boku
jest prostopadła do boku 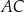 oraz
oraz 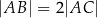 . Oblicz miarę kąta
. Oblicz miarę kąta 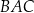 .
.
W trójkącie 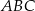 dane są kąt
dane są kąt 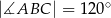 ,
, 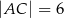 i
i 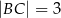 . Dwusieczna kąta
. Dwusieczna kąta 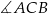 przecina bok
przecina bok 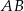 w punkcie
w punkcie 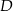 . Oblicz długość odcinka
. Oblicz długość odcinka 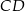 .
.
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 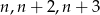 jest rozwartokątny.
jest rozwartokątny.
W trójkącie 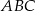 , w którym
, w którym 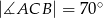 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 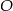 z wierzchołkami
z wierzchołkami 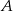 i
i 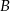 . Oblicz miarę kąta
. Oblicz miarę kąta 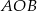 .
.
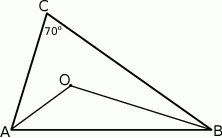
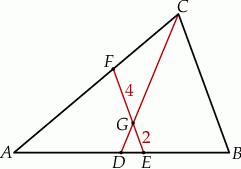
W trójkącie 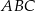 odcinek
odcinek 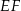 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 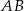 i
i 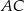 przecina środkową
przecina środkową 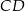 w punkcie
w punkcie 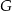 , oraz odcinek
, oraz odcinek 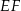 jest równoległy do odcinka
jest równoległy do odcinka 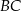 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 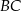 wiedząc, że
wiedząc, że 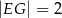 i
i 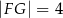 .
.
Każdy kąt trójkąta 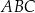 ma miarę mniejszą niż
ma miarę mniejszą niż 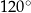 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 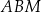 ,
, 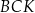 i
i 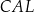 (zobacz rysunek).
(zobacz rysunek).
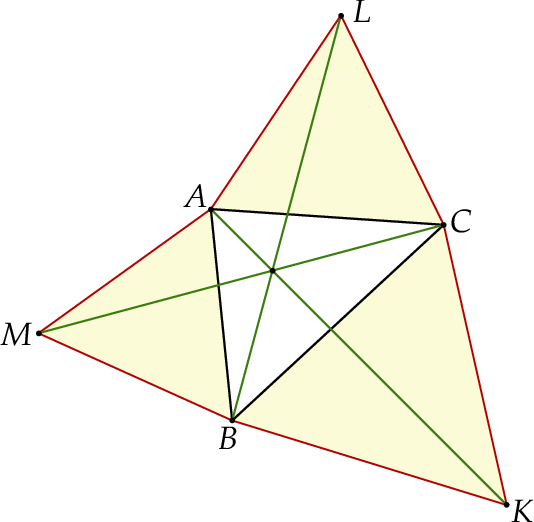
-
Wykaż, że
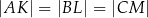 .
. -
Wykaż, że proste
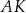 ,
, 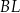 i
i 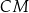 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
Okrąg o promieniu 4 jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków na odcinki o długości 6 i 8. Oblicz długości boków tego trójkąta.
W trójkącie 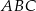 długości boków
długości boków 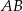 i
i 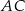 są odpowiednio równe 4 i 6. Punkt
są odpowiednio równe 4 i 6. Punkt 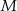 jest środkiem odcinka
jest środkiem odcinka 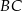 , a długość środkowej
, a długość środkowej 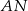 trójkąta
trójkąta 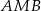 jest równa 3. Oblicz długość boku
jest równa 3. Oblicz długość boku 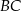 .
.
Promień okręgu opisanego na trójkącie 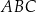 jest równy 17. Najdłuższym bokiem tego trójkąta jest bok
jest równy 17. Najdłuższym bokiem tego trójkąta jest bok 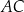 , a długości dwóch pozostałych boków są równe
, a długości dwóch pozostałych boków są równe 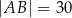 oraz
oraz 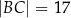 . Oblicz miarę kąta
. Oblicz miarę kąta 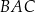 oraz długość boku
oraz długość boku 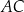 tego trójkąta.
tego trójkąta.
Jeden z boków trójkąta ma długość  , zaś kąty trójkąta przyległe do tego boku mają miary
, zaś kąty trójkąta przyległe do tego boku mają miary  i
i 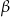 . Znajdź promień okręgu wpisanego w ten trójkąt.
. Znajdź promień okręgu wpisanego w ten trójkąt.
W trójkącie 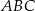 dane są długości boków
dane są długości boków 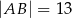 i
i 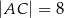 oraz
oraz 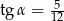 , gdzie
, gdzie 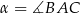 . Oblicz pole trójkąta
. Oblicz pole trójkąta 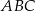 .
.
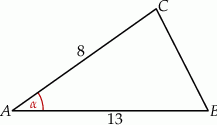
W trójkącie 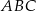 długość boku
długość boku 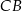 stanowi
stanowi 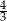 długości boku
długości boku 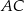 , a kąt
, a kąt 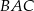 ma miarę
ma miarę 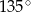 . Oblicz cosinus kąta
. Oblicz cosinus kąta 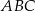 .
.

