W trójkącie równoramiennym dane są długości podstawy 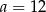 cm i wysokości
cm i wysokości 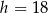 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Równoramienny
Odcinek 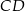 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 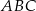 , w którym
, w którym 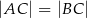 . Punkt
. Punkt 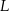 jest rzutem punktu
jest rzutem punktu 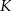 wysokości
wysokości 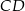 na bok
na bok 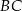 . Udowodnij, że
. Udowodnij, że 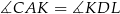 .
.
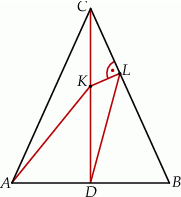
Odcinek 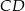 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 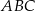 , w którym
, w którym 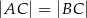 . Punkt
. Punkt 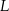 jest rzutem punktu
jest rzutem punktu 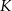 wysokości
wysokości 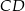 na bok
na bok 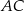 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 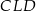 jest podobny do trójkąta
jest podobny do trójkąta 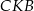 .
.
Na ramionach  i
i  trójkąta równoramiennego
trójkąta równoramiennego  wybrano punkty
wybrano punkty 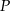 i
i 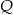 w ten sposób, że odcinek
w ten sposób, że odcinek 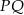 jest równoległy do podstawy
jest równoległy do podstawy 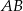 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 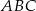 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 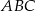 jest równe
jest równe
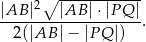
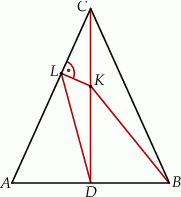
Punkt 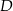 leży na boku
leży na boku 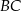 trójkąta równoramiennego
trójkąta równoramiennego 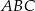 , w którym
, w którym 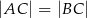 .
.
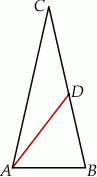
Odcinek 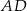 dzieli trójkąt
dzieli trójkąt 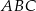 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 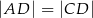 oraz
oraz 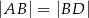 . Udowodnij, że
. Udowodnij, że 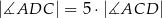 .
.
Punkt 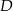 leży na boku
leży na boku 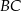 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 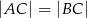 . Odcinek
. Odcinek 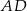 dzieli trójkąt
dzieli trójkąt 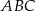 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 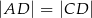 i
i 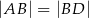 . Wykaż, że
. Wykaż, że 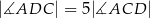 .
.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 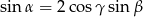 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.

