Największy internetowy zbiór zadań z matematyki
W metalowym ostrosłupie prawidłowym czworokątnym o wysokości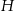 
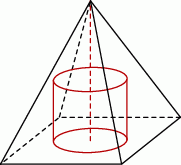
i krawędzi podstawy 
wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?
Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa 80, pole powierzchni całkowitej jest równe 256 i długości wszystkich krawędzi są nie mniejsze niż 4. Objętość 
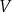każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji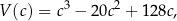
gdzie ![[ ] c ∈ 4, 238](https://img.zadania.info/zad/2512356/HzadT2x.png)
jest długością jednej z krawędzi bryły. Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza.
Na półkuli o promieniu 
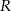opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
W ostrosłup prawidłowy czworokątny o wysokości 
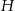wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
