Czworokąt 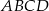 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 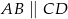 . Wykaż że
. Wykaż że
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Czworokąt 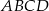 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 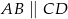 . Wykaż że
. Wykaż że
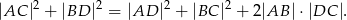
W trapez 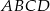 , gdzie
, gdzie 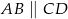 i
i 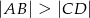 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
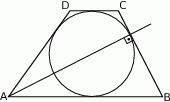
Dwusieczna kąta ostrego przy wierzchołku 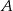 jest prostopadła do ramienia
jest prostopadła do ramienia 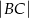 .
.
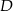 jest równoległa do ramienia
jest równoległa do ramienia 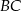 .
. 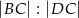 .
.Czworokąt 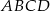 jest trapezem o podstawach
jest trapezem o podstawach 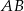 i
i 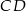 . Wykaż że
. Wykaż że
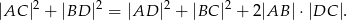
Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 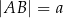 i
i 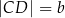 .
.
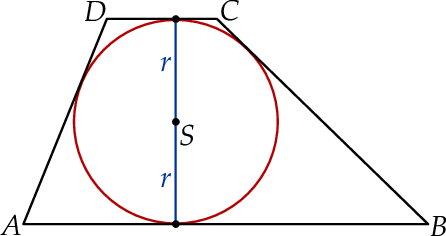
Wykaż, że 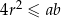 .
.
Ramiona trapezu są średnicami dwóch okręgów. Wykaż, że jeśli okręgi te są styczne zewnętrznie, to w trapez ten można wpisać okrąg.
Punkt 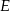 leży na ramieniu
leży na ramieniu 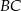 trapezu
trapezu 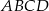 , w którym
, w którym 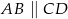 . Udowodnij, że
. Udowodnij, że 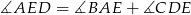 .
.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
