Parabola o równaniu 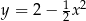 przecina oś
przecina oś 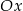 układu współrzędnych w punktach
układu współrzędnych w punktach 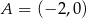 i
i 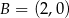 . Rozpatrujemy wszystkie trapezy równoramienne
. Rozpatrujemy wszystkie trapezy równoramienne 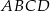 , których dłuższą podstawą jest odcinek
, których dłuższą podstawą jest odcinek 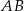 , a końce
, a końce 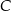 i
i 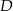 krótszej podstawy leżą na paraboli (zobacz rysunek).
krótszej podstawy leżą na paraboli (zobacz rysunek).
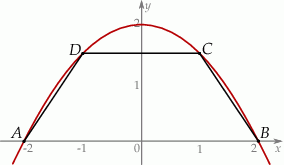
Wyznacz pole trapezu 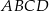 w zależności od pierwszej współrzędnej wierzchołka
w zależności od pierwszej współrzędnej wierzchołka 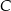 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 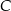 tego z rozpatrywanych trapezów, którego pole jest największe.
tego z rozpatrywanych trapezów, którego pole jest największe.

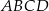 , których dwa wierzchołki
, których dwa wierzchołki 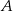 i
i 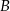 leżą na odcinku o końcach
leżą na odcinku o końcach 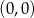 i
i 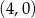 , a dwa pozostałe wierzchołki
, a dwa pozostałe wierzchołki 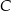 i
i 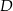 leżą na paraboli o równaniu
leżą na paraboli o równaniu 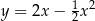 (zobacz rysunek).
(zobacz rysunek). 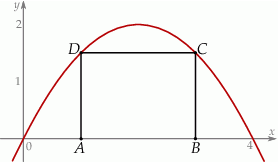
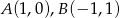 . Punkt
. Punkt 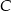 należy do okręgu o równaniu
należy do okręgu o równaniu 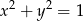 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 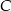 tak, aby pole trójkąta
tak, aby pole trójkąta 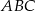 było największe. Oblicz to pole.
było największe. Oblicz to pole. 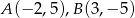 . Punkt
. Punkt 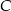 należy do okręgu o równaniu
należy do okręgu o równaniu 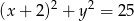 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 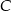 tak, aby pole trójkąta
tak, aby pole trójkąta 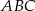 było największe. Oblicz to pole.
było największe. Oblicz to pole. 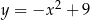 . Na tej paraboli leży punkt
. Na tej paraboli leży punkt 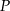 o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie
o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie 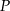 ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu. 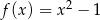 określona dla
określona dla 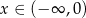 . W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.
. W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole. 