Dla dowolnej liczby 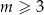 , prosta
, prosta 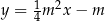 przecina hiperbolę
przecina hiperbolę 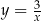 w punktach
w punktach 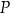 i
i 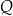 . Uzasadnij, że
. Uzasadnij, że 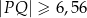 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum
Na rysunku poniżej przedstawiono fragment wykresu funkcji 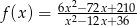 określonej dla
określonej dla 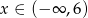 . Wykres ten przecina osie
. Wykres ten przecina osie 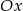 i
i 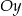 odpowiednio w punktach
odpowiednio w punktach 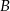 i
i 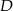 , a punkt
, a punkt 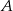 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 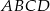 , w których punkt
, w których punkt 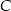 leży na wykresie funkcji
leży na wykresie funkcji 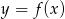 pomiędzy punktami
pomiędzy punktami  i
i  .
.
Oblicz pierwszą współrzędną wierzchołka  tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.
Prosta 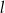 , na której leży punkt
, na której leży punkt 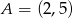 , przecina parabolę o równaniu
, przecina parabolę o równaniu 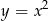 w dwóch różnych punktach
w dwóch różnych punktach 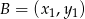 i
i 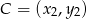 . Oblicz wartość współczynnika kierunkowego prostej
. Oblicz wartość współczynnika kierunkowego prostej 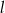 , przy której suma
, przy której suma 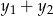 osiągnie wartość najmniejszą.
osiągnie wartość najmniejszą.
Dane są punkty 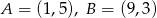 i prosta
i prosta 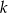 o równaniu
o równaniu 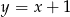 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 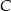 leżącego na prostej
leżącego na prostej 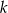 , dla którego suma
, dla którego suma 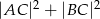 jest najmniejsza.
jest najmniejsza.
Na płaszczyźnie dane są punkty 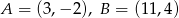 . Na prostej o równaniu
. Na prostej o równaniu 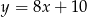 znajdź punkt
znajdź punkt 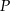 , dla którego suma
, dla którego suma 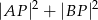 jest najmniejsza.
jest najmniejsza.
Wyznacz współrzędne punktu 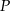 leżącego na prostej o równaniu
leżącego na prostej o równaniu 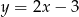 , którego suma kwadratów odległości od punktów
, którego suma kwadratów odległości od punktów 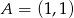 i
i 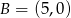 jest najmniejsza.
jest najmniejsza.
Na prostej o równaniu 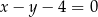 znajdź punkt
znajdź punkt  , którego kwadrat odległości od punktu
, którego kwadrat odległości od punktu 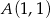 jest najmniejszy.
jest najmniejszy.
Na prostej o równaniu 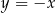 wyznacz współrzędne punktu
wyznacz współrzędne punktu 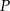 leżącego najbliżej punktu
leżącego najbliżej punktu 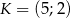 .
.
Na prostej o równaniu 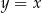 wyznacz współrzędne punktu
wyznacz współrzędne punktu 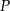 leżącego najbliżej punktu
leżącego najbliżej punktu 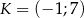 .
.
Na prostej 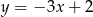 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Wyznacz współrzędne punktu 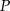 leżącego na wykresie funkcji
leżącego na wykresie funkcji 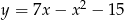 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
, dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
Dany jest ciąg punktów 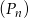 na płaszczyźnie, których współrzędne dane są wzorem
na płaszczyźnie, których współrzędne dane są wzorem 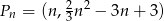 , gdzie
, gdzie 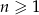 . Wyznacz tę wartość
. Wyznacz tę wartość  , dla której odległość punktu
, dla której odległość punktu 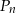 od prostej
od prostej 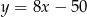 jest najmniejsza z możliwych.
jest najmniejsza z możliwych.
Dane są punkty 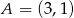 i
i 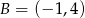 oraz prosta
oraz prosta 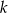 o równaniu
o równaniu 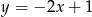 . Wyznacz taki punkt
. Wyznacz taki punkt 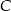 prostej
prostej 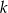 , aby suma kwadratów boków trójkąta
, aby suma kwadratów boków trójkąta 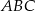 była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.
była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.
Który z odcinków łączących dowolny punkt paraboli o równaniu 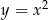 z punktem
z punktem 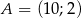 ma najmniejszy kwadrat długości?
ma najmniejszy kwadrat długości?
Wyznacz te punkty paraboli 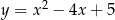 , które znajdują się najbliżej punktu
, które znajdują się najbliżej punktu 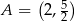 . Oblicz tę najmniejszą odległość.
. Oblicz tę najmniejszą odległość.
Rozpatrujemy prostokąty  , których dwa wierzchołki leżą na osi
, których dwa wierzchołki leżą na osi  , jeden wierzchołek leży na paraboli określonej równaniem
, jeden wierzchołek leży na paraboli określonej równaniem 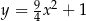 , jeden wierzchołek leży na wykresie funkcji
, jeden wierzchołek leży na wykresie funkcji 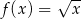 określonej dla
określonej dla 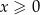 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
. Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
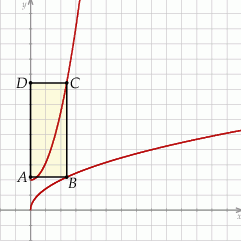
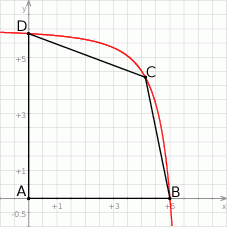
Rozpatrujemy wszystkie trapezy  , których wierzchołki
, których wierzchołki 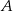 i
i 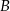 leżą na wykresie funkcji
leżą na wykresie funkcji 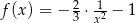 określonej dla
określonej dla 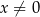 . Punkt
. Punkt 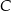 ma współrzędne
ma współrzędne 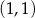 , a oś
, a oś 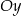 jest osią symetrii tego trapezu (zobacz rysunek).
jest osią symetrii tego trapezu (zobacz rysunek).
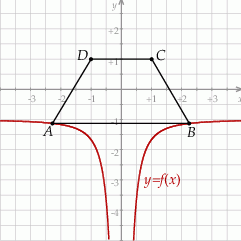
Oblicz obwód tego trapezu 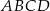 , którego pole jest najmniejsze możliwe.
, którego pole jest najmniejsze możliwe.
Dwa wierzchołki prostokąta leżą na osi  , a pozostałe dwa należą do paraboli o równaniu
, a pozostałe dwa należą do paraboli o równaniu 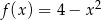 i znajdują się powyżej osi
i znajdują się powyżej osi  .
.
- Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego podstawy.
- Dla jakiej długości podstawy pole tego prostokąta jest równe 6.
- Dla jakiej długości podstawy pole tego prostokąta jest największe?
Dana jest parabola opisana równaniem 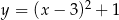 . Tworzymy trójkąty
. Tworzymy trójkąty 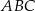 takie, że punkt
takie, że punkt 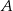 leży w początku układu współrzędnych, punkt
leży w początku układu współrzędnych, punkt 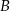 o współrzędnych
o współrzędnych 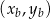 leży na paraboli, punkt
leży na paraboli, punkt 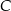 ma współrzędne
ma współrzędne 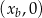 .
.
- Napisz wzór funkcji
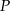 , określającej pole trójkąta
, określającej pole trójkąta 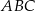 w zależności od
w zależności od 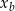 dla
dla 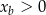 .
. - Znajdź trójkąt o największym polu dla
![xb ∈ [0;2]](https://img.zadania.info/zad/3724416/HzadT11x.gif) ; w odpowiedzi podaj współrzędne punktu
; w odpowiedzi podaj współrzędne punktu 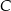 .
.
Na paraboli o równaniu 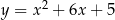 znajdź współrzędne punktu
znajdź współrzędne punktu 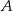 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 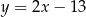 jest najmniejsza.
jest najmniejsza.
Na paraboli o równaniu 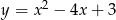 wyznacz punkt, którego odległość od prostej
wyznacz punkt, którego odległość od prostej 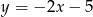 jest najmniejsza.
jest najmniejsza.
Dany jest trójkąt 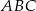 , w którym
, w którym 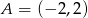 i
i 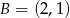 . Wierzchołek
. Wierzchołek 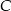 leży na prostej o równaniu
leży na prostej o równaniu 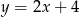 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 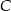 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
Dany jest trójkąt 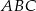 , w którym
, w którym 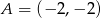 i
i 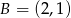 . Wierzchołek
. Wierzchołek 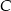 leży na prostej o równaniu
leży na prostej o równaniu 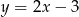 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 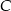 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
Wyznacz wartość parametru 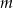 , dla której odległość punktu
, dla której odległość punktu 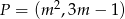 od prostej
od prostej 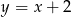 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Rozważamy trójkąty 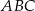 , w których
, w których 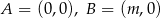 , gdzie
, gdzie 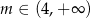 , a wierzchołek
, a wierzchołek 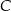 leży na prostej o równaniu
leży na prostej o równaniu 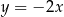 . Na boku
. Na boku 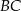 tego trójkąta leży punkt
tego trójkąta leży punkt 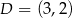 .
.
- Wykaż, że dla
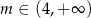 pole
pole 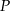 trójkąta
trójkąta 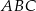 , jako funkcja zmiennej
, jako funkcja zmiennej 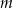 , wyraża się wzorem
, wyraża się wzorem 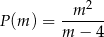
- Oblicz tę wartość
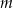 , dla której funkcja
, dla której funkcja 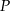 osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej 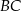 , przy której funkcja
, przy której funkcja  osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/5154135/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 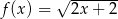 i
i 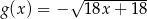 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 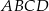 , których wierzchołki
, których wierzchołki 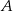 i
i 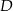 leżą na wykresie funkcji
leżą na wykresie funkcji 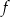 , a wierzchołki
, a wierzchołki 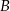 i
i 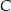 leżą na wykresie funkcji
leżą na wykresie funkcji 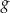 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 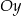 (zobacz rysunek).
(zobacz rysunek).
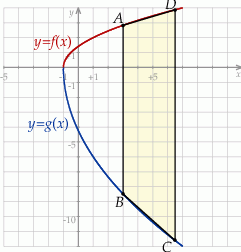
Oblicz współrzędne wierzchołków tego z rozpatrywanych trapezów, w którym 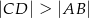 , i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka
, i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka 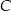 trapezu
trapezu 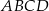 jest równa 7, a druga współrzędna wierzchołka
jest równa 7, a druga współrzędna wierzchołka 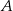 jest równa
jest równa 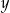 , to pole trapezu wyraża się wzorem
, to pole trapezu wyraża się wzorem
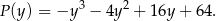
Znajdź taki punkt 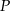 leżący na prostej
leżący na prostej 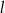 o równaniu
o równaniu 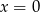 , z którego odcinek
, z którego odcinek 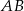 , gdzie
, gdzie 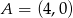 ,
, 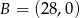 , widać pod możliwie największym kątem. Wyznacz ten kąt.
, widać pod możliwie największym kątem. Wyznacz ten kąt.

