Stopnia 4/Wielomianowe/Równania - zadania z matematyki

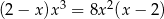/Szkoła średnia/Równania/Wielomianowe/Stopnia 4

Wykaż, że równanie 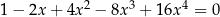2 3 4 1 − 2x + 4x − 8x + 16x = 0 nie ma rozwiązań rzeczywistych.

Dla jakich wartości parametru 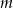zbiór rozwiązań równania 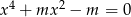4 2 x + mx − m = 0 jest dwuelementowy?

Wyznacz wszystkie liczby całkowite 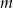, dla których równanie

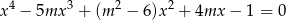
4 3 2 2 x − 5mx + (m − 6)x + 4mx − 1 = 0

nie ma rozwiązań wymiernych.

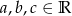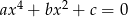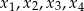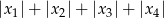Dane są liczby a,b,c ∈ R takie, że równanie 4 2 ax + bx + c = 0 ma cztery rozwiązania rzeczywiste x1,x2,x3,x4 . Oblicz wartość wyrażenia |x1|+ |x 2|+ |x3|+ |x4| .

Wyznacz wielomian czwartego stopnia 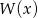W (x) wiedząc, że liczba 3 jest jego czterokrotnym pierwiastkiem oraz W (1) = 80 .

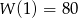Zbadaj, dla jakich wartości parametru 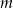równanie 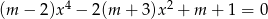4 2 (m − 2)x − 2(m + 3)x + m + 1 = 0 ma cztery różne pierwiastki rzeczywiste.

Ukryj Podobne zadania

Dana jest funkcja 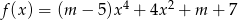4 2 f(x ) = (m − 5 )x + 4x + m + 7 , gdzie 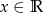x ∈ R . Wyznacz wszystkie wartości parametru 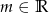m ∈ R , dla których funkcja ma 4 różne miejsca zerowe.

Rozwiąż równanie 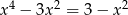4 2 2 x − 3x = 3 − x .

Ukryj Podobne zadania

Rozwiąż równanie 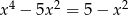4 2 2 x − 5x = 5 − x .

Oblicz sumę kwadratów pierwiastków równania 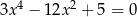4 2 3x − 12x + 5 = 0 .

Rozwiąż równanie 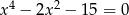4 2 x − 2x − 15 = 0 .

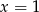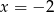Liczby x = 1 i x = − 2 są pierwiastkami wielomianu 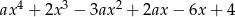4 3 2 ax + 2x − 3ax + 2ax − 6x + 4 . Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz .

Strona 2 z 2