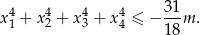Wykaż, że równanie 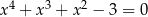 ma tylko jedno rozwiązanie które jest liczbą wymierną.
ma tylko jedno rozwiązanie które jest liczbą wymierną.
/Szkoła średnia/Równania/Wielomianowe/Stopnia 4
Wyznacz te wartości parametru 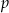 , dla których równanie
, dla których równanie 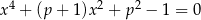 ma dokładnie dwa różne pierwiastki.
ma dokładnie dwa różne pierwiastki.
Dla jakich wartości parametru 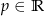 równanie
równanie 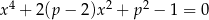 ma dokładnie dwa różne rozwiązania?
ma dokładnie dwa różne rozwiązania?
Wyznacz te wartości parametru 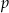 , dla których równanie
, dla których równanie 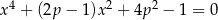 ma dokładnie dwa różne pierwiastki rzeczywiste.
ma dokładnie dwa różne pierwiastki rzeczywiste.
Rozwiąż równanie 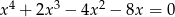 .
.
Rozwiąż równanie 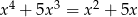 .
.
Rozwiąż równanie 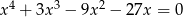 .
.
Dla jakich wartości parametru 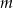 wielomian
wielomian 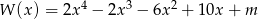 ma pierwiastek trzykrotny?
ma pierwiastek trzykrotny?
Wykaż, że równanie 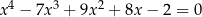 ma w przedziale
ma w przedziale 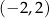 co najmniej dwa różne rozwiązania.
co najmniej dwa różne rozwiązania.
Rozwiąż równanie 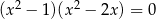 .
.
Rozwiąż równanie 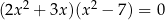 .
.
Rozwiąż równanie 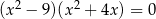 .
.
Rozważmy równanie 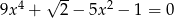 .
.
- Uzasadnij, że równanie to ma 4 pierwiastki.
- Oblicz sumę szóstych potęg wszystkich pierwiastków tego równania.
Liczby 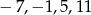 są miejscami zerowymi wielomianu czwartego stopnia
są miejscami zerowymi wielomianu czwartego stopnia 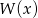 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest równość
spełniona jest równość 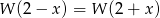 .
.
Dla jakich wartości parametru 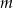 równanie
równanie ![2 2 (x − m ) [m(x − m ) − m − 1]+ 1 = 0](https://img.zadania.info/zad/3650840/HzadT1x.gif) ma więcej pierwiastków dodatnich niż ujemnych?
ma więcej pierwiastków dodatnich niż ujemnych?
Wyznacz wszystkie wartości parametru 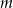 , dla których wielomian
, dla których wielomian
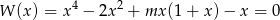
ma 4 różne pierwiastki.
Rozwiąż równanie 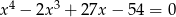 .
.
Wielomian 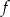 jest określony wzorem
jest określony wzorem 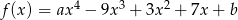 dla pewnych liczb pierwszych
dla pewnych liczb pierwszych  oraz
oraz 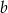 . Wiadomo, ze liczba
. Wiadomo, ze liczba  jest pierwiastkiem tego wielomianu. Oblicz
jest pierwiastkiem tego wielomianu. Oblicz  i
i 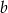 .
.
Rozwiąż równanie 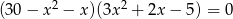 .
.
Wyznacz wszystkie wartości parametru 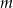 , dla których równanie
, dla których równanie
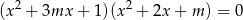
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
Rozwiąż równanie 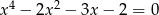 .
.
Dobierz wartości 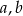 i
i  tak, aby liczby
tak, aby liczby 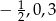 były pierwiastkami wielomianu
były pierwiastkami wielomianu 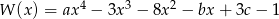 .
.
Pierwiastki wielomianu 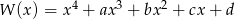 tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że
tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że 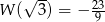 . Oblicz współczynniki
. Oblicz współczynniki 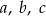 i
i 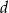 . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Wyznacz wartości parametrów  i
i 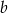 dla których jedynymi rozwiązaniami równania
dla których jedynymi rozwiązaniami równania
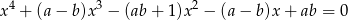
są liczby 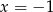 i
i 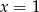 .
.
Rozwiąż równanie 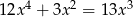 .
.
Wyznacz wszystkie wartości parametru 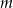 , dla których równanie
, dla których równanie 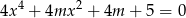 ma cztery różne pierwiastki rzeczywiste spełniające warunek
ma cztery różne pierwiastki rzeczywiste spełniające warunek