Na boku 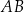 trójkąta
trójkąta 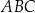 wybrano punkt
wybrano punkt 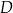 w ten sposób, że
w ten sposób, że 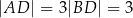 . Bok
. Bok 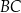 tego trójkąta ma długość 2. Oblicz stosunek długości odcinków
tego trójkąta ma długość 2. Oblicz stosunek długości odcinków 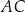 i
i 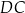 .
.

 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na boku 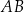 trójkąta
trójkąta 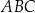 wybrano punkt
wybrano punkt 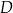 w ten sposób, że
w ten sposób, że 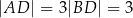 . Bok
. Bok 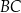 tego trójkąta ma długość 2. Oblicz stosunek długości odcinków
tego trójkąta ma długość 2. Oblicz stosunek długości odcinków 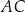 i
i 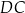 .
.

W trójkącie ostrokątnym 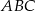 dane są długości boków:
dane są długości boków: 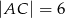 ,
, 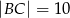 . Pole trójkąta jest równe
. Pole trójkąta jest równe 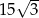 . Oblicz
. Oblicz
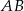 ;
; 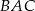 ;
; 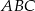 ;
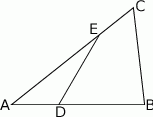
; Na bokach 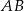 i
i 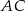 trójkąta
trójkąta 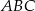 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 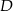 i
i 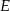 , że
, że 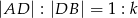 oraz
oraz 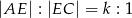 , dla
, dla 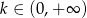 .
.
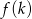 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 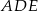 i
i 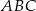 .
. 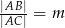 , dla
, dla 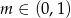 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 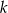 , dla których trójkąty
, dla których trójkąty 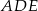 i
i 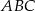 są podobne.
są podobne.