Dany jest wielomian 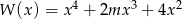 z parametrem
z parametrem 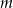 .
.
- Wiedząc, że wykres tego wielomianu jest symetryczny względem prostej
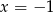 , wyznacz
, wyznacz 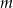 .
. - Dla wyznaczonej wartości parametru
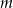 uzasadnij, że nierówność
uzasadnij, że nierówność 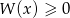 jest spełniona przez każdą liczbę rzeczywistą
jest spełniona przez każdą liczbę rzeczywistą 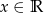 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest wielomian 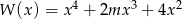 z parametrem
z parametrem 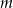 .
.
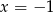 , wyznacz
, wyznacz 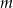 .
. 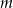 uzasadnij, że nierówność
uzasadnij, że nierówność 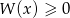 jest spełniona przez każdą liczbę rzeczywistą
jest spełniona przez każdą liczbę rzeczywistą 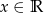 .
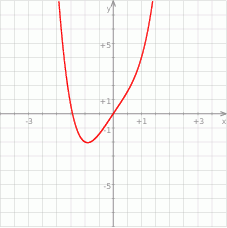
.Korzystając z danego wykresu funkcji 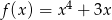 naszkicuj wykres funkcji
naszkicuj wykres funkcji 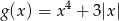 .
.
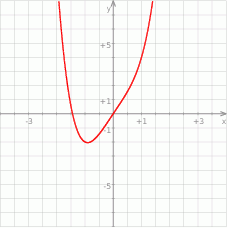
Korzystając z danego wykresu funkcji 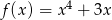 naszkicuj wykres funkcji
naszkicuj wykres funkcji 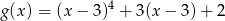 .
.
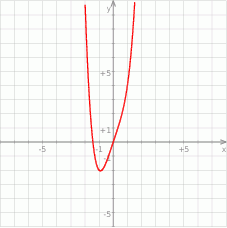
Korzystając z danego wykresu funkcji 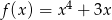 naszkicuj wykres funkcji
naszkicuj wykres funkcji 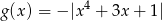 .
.
Funkcja 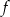 określona jest wzorem
określona jest wzorem 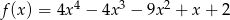 .
.
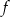 z osia
z osia 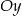 .
. 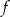 z osia
z osia 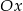 .
. 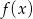 i funkcja
i funkcja 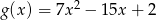 przyjmują tę samą wartość.
przyjmują tę samą wartość.